Probabilistic forecasting: prediction intervals and prediction distribution¶
When trying to anticipate future values, most forecasting models try to predict what will be the most likely value. This is called point-forecasting. Although knowing in advance the expected value of a time series is useful in almost every business case, this kind of prediction does not provide any information about the confidence of the model nor the prediction uncertainty.
Probabilistic forecasting, as opposed to point-forecasting, is a family of techniques that allow for predicting the expected distribution of the outcome instead of a single future value. This type of forecasting provides much rich information since it allows for creating prediction intervals, the range of likely values where the true value may fall. More formally, a prediction interval defines the interval within which the true value of the response variable is expected to be found with a given probability.
There are multiple ways to estimate prediction intervals, most of which require that the residuals (errors) of the model follow a normal distribution. When this property cannot be assumed, two alternatives commonly used are bootstrapping and quantile regression. To illustrate how skforecast allows estimating prediction intervals for multi-step forecasting, the following examples are shown:
Prediction intervals based on bootstrapped residuals and recursive-multi-step forecaster.
Prediction intervals based on quantile regression and direct-multi-step forecaster.
All forecasters in skforecast have four different methods that allow for probabilistic forecasting:
predict_bootstrapping: this method generates multiple forecasting predictions through a bootstrapping process. By sampling from a collection of past observed errors (the residuals), each bootstrapping iteration generates a different set of predictions. The output is apandas DataFramewith one row for each predicted step and one column for each bootstrapping iteration.predict_intervals: this method estimates quantile prediction intervals using the values generated withpredict_bootstrapping.predict_quantiles: this method estimates a list of quantile predictions using the values generated withpredict_bootstrapping.predict_dist: this method fits a parametric distribution using the values generated withpredict_bootstrapping. Any of the continuous distributions available in scipy.stats can be used.
The four can use in-sample residuals (default) or out-sample residuals. In both cases, the residuals can be conditioned on the predicted value to try to account for the existence of a correlation between the predicted values and the residuals.
⚠ Warning
As Rob J Hyndman explains in his blog, in real-world problems, almost all prediction intervals are too narrow. For example, nominal 95% intervals may only provide coverage between 71% and 87%. This is a well-known phenomenon and arises because they do not account for all sources of uncertainty. With forecasting models, there are at least four sources of uncertainty:
- The random error term
- The parameter estimates
- The choice of model for the historical data
- The continuation of the historical data generating process into the future
When producing prediction intervals for time series models, generally only the first of these sources is taken into account. Therefore, it is advisable to use test data to validate the empirical coverage of the interval and not solely rely on the expected coverage.
✎ Note
Conformal prediction is a relatively new framework that allows for the creation of confidence measures for predictions made by machine learning models. This method is on the roadmap of skforecast, but not yet available.
Prediction intervals using bootstrapped residuals¶
The error of a one-step-ahead forecast is defined as the difference between the actual value and the predicted value (et=yt−ˆyt|t−1et=yt−^yt|t−1). By assuming that future errors will be similar to past errors, it is possible to simulate different predictions by taking samples from the collection of errors previously seen in the past (i.e., the residuals) and adding them to the predictions.
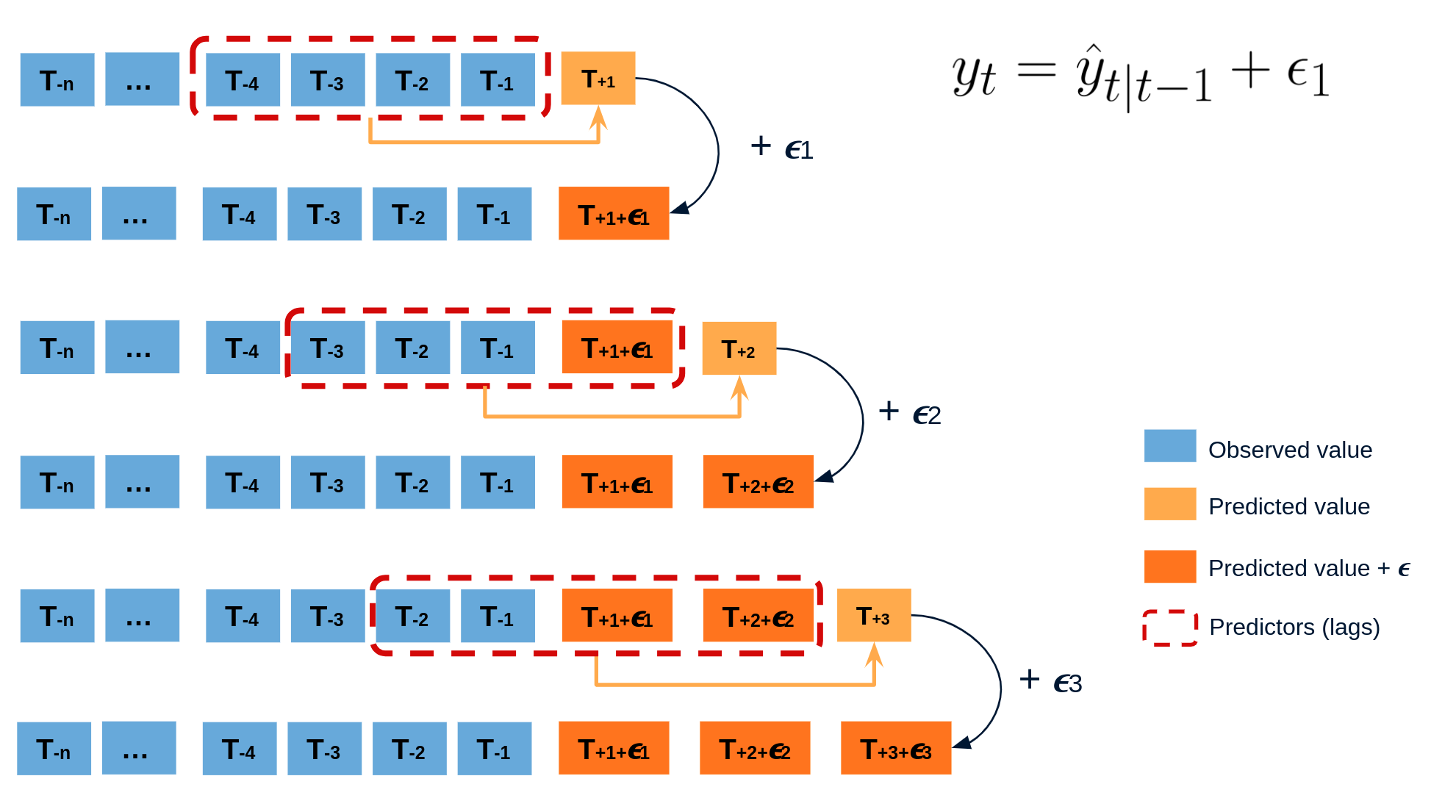
Diagram bootstrapping prediction process.
Repeatedly performing this process creates a collection of slightly different predictions, which represent the distribution of possible outcomes due to the expected variance in the forecasting process.
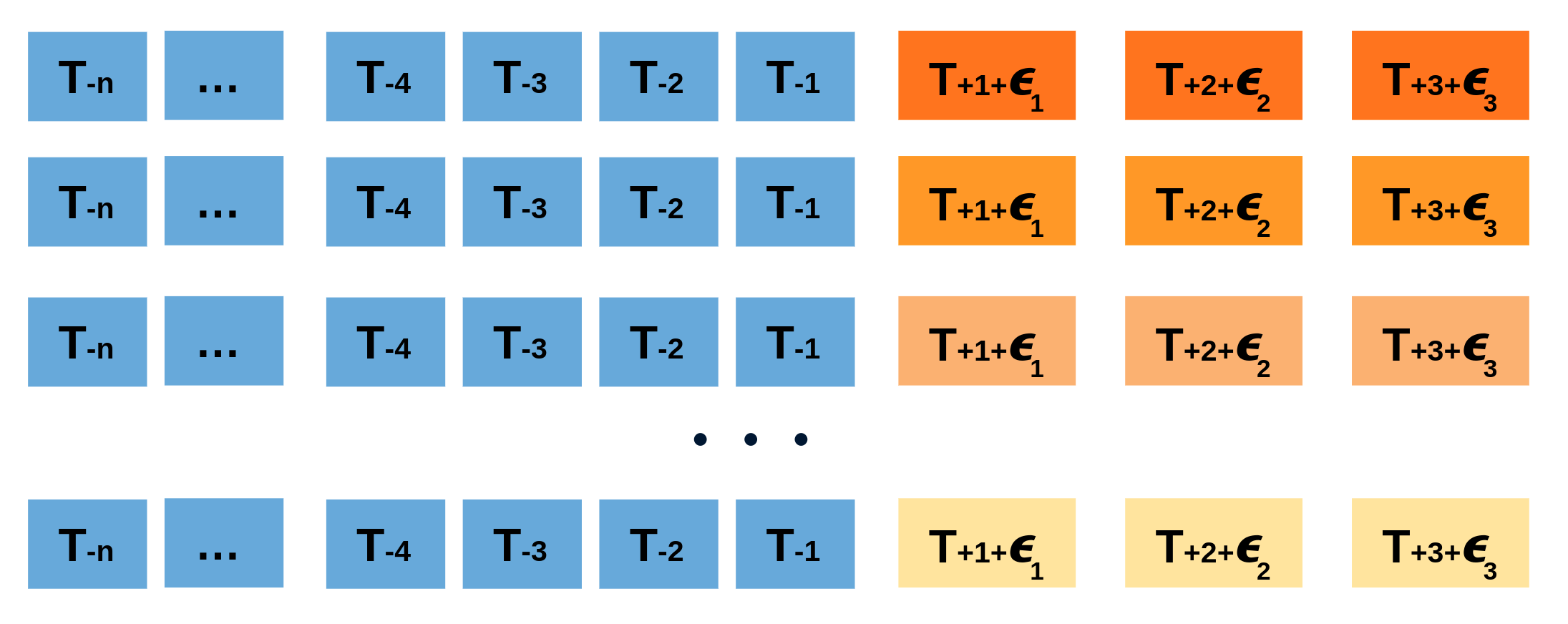
Bootstrapping predictions.
Using the outcome of the bootstrapping process, prediction intervals can be computed by calculating the α/2α/2 and 1−α/21−α/2 percentiles at each forecasting horizon.
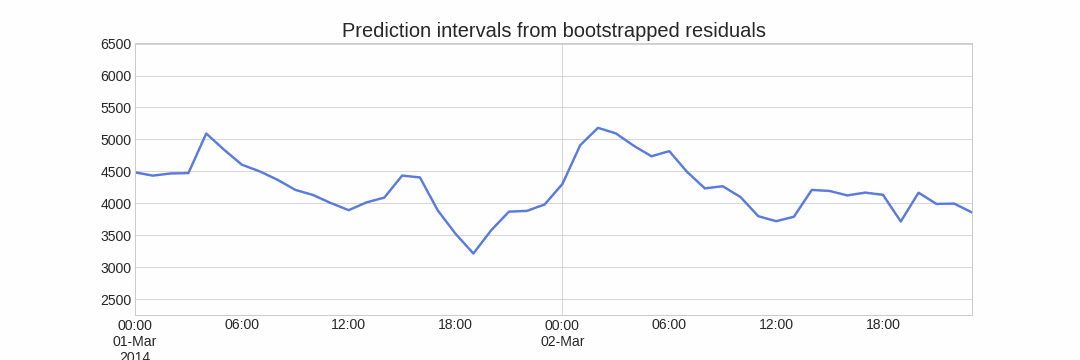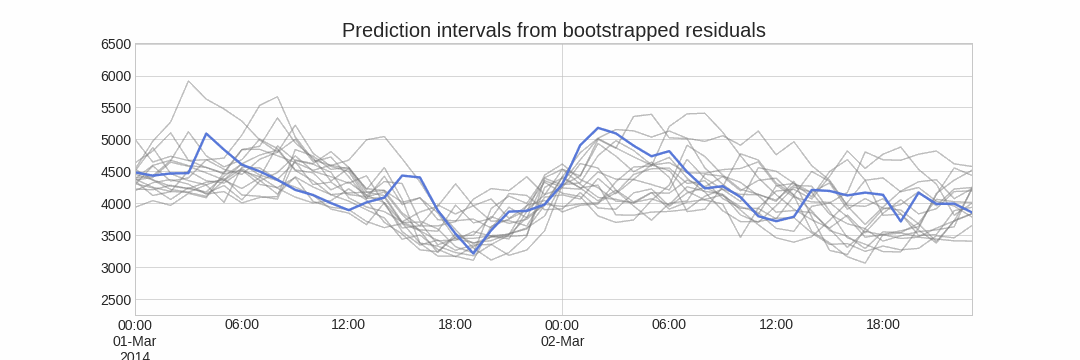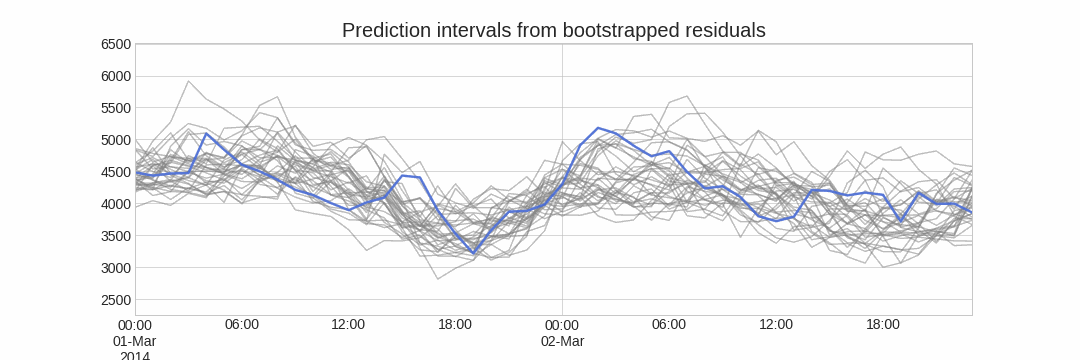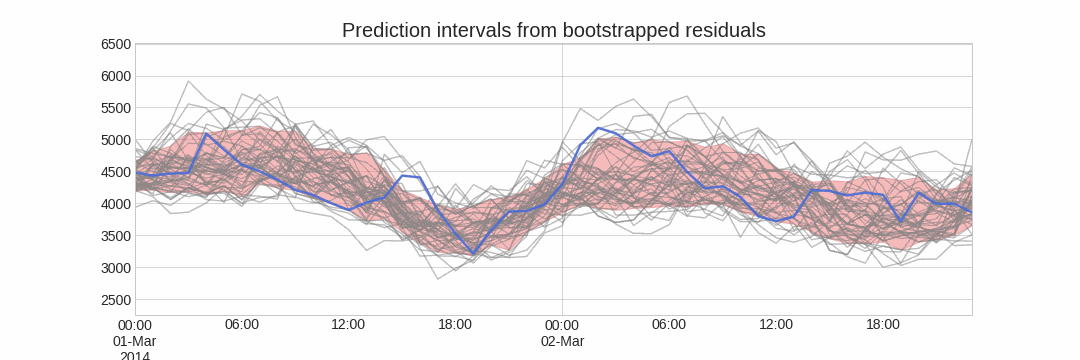
Alternatively, it is also possible to fit a parametric distribution for each forecast horizon.
One of the main advantages of this strategy is that it requires only a single model to estimate any interval. However, performing hundreds or thousands of bootstrapping iterations can be computationally expensive and may not always be feasible.
Libraries and data¶
# Data processing
# ==============================================================================
import numpy as np
import pandas as pd
from skforecast.datasets import fetch_dataset
# Plots
# ==============================================================================
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from skforecast.plot import plot_residuals
from skforecast.plot import plot_prediction_distribution
from skforecast.plot import plot_prediction_intervals
from pprint import pprint
# Modelling and Forecasting
# ==============================================================================
from scipy.stats import norm
from lightgbm import LGBMRegressor
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer
from sklearn.metrics import mean_pinball_loss
from skforecast.recursive import ForecasterRecursive
from skforecast.direct import ForecasterDirect
from skforecast.model_selection import TimeSeriesFold
from skforecast.model_selection import backtesting_forecaster
# Configuration
# ==============================================================================
import warnings
warnings.filterwarnings('once')
plt.style.use('seaborn-v0_8-darkgrid')
⚠ Warning
To create a sufficiently illustrative user guide, the data download process takes about 1 minute, and some functions called during the guide may take a few seconds to run. We appreciate your patience.
# Data download
# ==============================================================================
data = fetch_dataset(name='bike_sharing_extended_features')
data.head(2)
bike_sharing_extended_features ------------------------------ Hourly usage of the bike share system in the city of Washington D.C. during the years 2011 and 2012. In addition to the number of users per hour, the dataset was enriched by introducing supplementary features. Addition includes calendar- based variables (day of the week, hour of the day, month, etc.), indicators for sunlight, incorporation of rolling temperature averages, and the creation of polynomial features generated from variable pairs. All cyclic variables are encoded using sine and cosine functions to ensure accurate representation. Fanaee-T,Hadi. (2013). Bike Sharing Dataset. UCI Machine Learning Repository. https://doi.org/10.24432/C5W894. Shape of the dataset: (17352, 90)
| users | weather | month_sin | month_cos | week_of_year_sin | week_of_year_cos | week_day_sin | week_day_cos | hour_day_sin | hour_day_cos | ... | temp_roll_mean_1_day | temp_roll_mean_7_day | temp_roll_max_1_day | temp_roll_min_1_day | temp_roll_max_7_day | temp_roll_min_7_day | holiday_previous_day | holiday_next_day | temp | holiday | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| date_time | |||||||||||||||||||||
| 2011-01-08 00:00:00 | 25.0 | mist | 0.5 | 0.866025 | 0.120537 | 0.992709 | -0.781832 | 0.62349 | 0.258819 | 0.965926 | ... | 8.063334 | 10.127976 | 9.02 | 6.56 | 18.86 | 4.92 | 0.0 | 0.0 | 7.38 | 0.0 |
| 2011-01-08 01:00:00 | 16.0 | mist | 0.5 | 0.866025 | 0.120537 | 0.992709 | -0.781832 | 0.62349 | 0.500000 | 0.866025 | ... | 8.029166 | 10.113334 | 9.02 | 6.56 | 18.86 | 4.92 | 0.0 | 0.0 | 7.38 | 0.0 |
2 rows × 90 columns
# One hot encoding of categorical variables
# ==============================================================================
encoder = ColumnTransformer(
[('one_hot_encoder', OneHotEncoder(sparse_output=False), ['weather'])],
remainder='passthrough',
verbose_feature_names_out=False
).set_output(transform="pandas")
data = encoder.fit_transform(data)
# Select exogenous variables to be included in the model
# ==============================================================================
exog_features = [
'weather_clear', 'weather_mist', 'weather_rain', 'month_sin', 'month_cos',
'week_of_year_sin', 'week_of_year_cos', 'week_day_sin', 'week_day_cos',
'hour_day_sin', 'hour_day_cos', 'sunrise_hour_sin', 'sunrise_hour_cos',
'sunset_hour_sin', 'sunset_hour_cos', 'temp', 'holiday'
]
data = data[['users'] + exog_features]
# Split train-validation-test
# ==============================================================================
data = data.loc['2011-05-30 23:59:00':, :]
end_train = '2012-08-30 23:59:00'
end_validation = '2012-11-15 23:59:00'
data_train = data.loc[: end_train, :]
data_val = data.loc[end_train:end_validation, :]
data_test = data.loc[end_validation:, :]
print(f"Dates train : {data_train.index.min()} --- {data_train.index.max()} (n={len(data_train)})")
print(f"Dates validacion : {data_val.index.min()} --- {data_val.index.max()} (n={len(data_val)})")
print(f"Dates test : {data_test.index.min()} --- {data_test.index.max()} (n={len(data_test)})")
Dates train : 2011-05-31 00:00:00 --- 2012-08-30 23:00:00 (n=10992) Dates validacion : 2012-08-31 00:00:00 --- 2012-11-15 23:00:00 (n=1848) Dates test : 2012-11-16 00:00:00 --- 2012-12-30 23:00:00 (n=1080)
# Plot time series partition
# ==============================================================================
fig, ax = plt.subplots(figsize=(9, 3))
data_train['users'].plot(label='train', ax=ax)
data_val['users'].plot(label='validation', ax=ax)
data_test['users'].plot(label='test', ax=ax)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_title('Number of users')
ax.legend();
Intervals with In-sample residuals¶
By default, intervals can be computed using in-sample residuals (residuals from the training set), either by calling the predict_interval() method, or by performing a full backtesting procedure. However, this can result in intervals that are too narrow (overly optimistic).
# Create and fit forecaster
# ==============================================================================
params = {
"n_estimators": 600,
"max_depth": 6,
"min_data_in_leaf": 88,
"learning_rate": 0.2520098236227423,
"feature_fraction": 0.6,
"max_bin": 75,
"reg_alpha": 1.0,
"reg_lambda": 0.8,
}
lags = 48
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(random_state=15926, verbose=-1, **params),
lags = lags
)
forecaster.fit(
y = data.loc[:end_validation, 'users'],
exog = data.loc[:end_validation, exog_features]
)
# In-sample residuals stored during fit
# ==============================================================================
print("Amount of residuals stored:", len(forecaster.in_sample_residuals_))
forecaster.in_sample_residuals_
Amount of residuals stored: 10000
array([-2.36857116, -2.77682126, -4.03075774, ..., -4.12456496,
4.45391786, 17.70362401])
# Predict interval with in-sample residuals
# ==============================================================================
predictions = forecaster.predict_interval(
exog = data_test[exog_features],
steps = 7,
interval = [10, 90]
)
predictions
| pred | lower_bound | upper_bound | |
|---|---|---|---|
| 2012-11-16 00:00:00 | 70.009970 | 53.587645 | 85.206036 |
| 2012-11-16 01:00:00 | 45.679914 | 30.385990 | 62.928811 |
| 2012-11-16 02:00:00 | 19.225220 | 2.777457 | 34.043910 |
| 2012-11-16 03:00:00 | -0.039409 | -15.202064 | 15.646154 |
| 2012-11-16 04:00:00 | 0.154831 | -14.950966 | 15.733683 |
| 2012-11-16 05:00:00 | 37.330998 | 25.131931 | 54.885782 |
| 2012-11-16 06:00:00 | 116.737843 | 69.809702 | 143.786683 |
The backtesting_forecaster() function is used to generate the prediction intervals for the entire test set and calculate coverage of a given interval.
use_in_sample_residuals = Trueis used to compute the intervals using in-sample residuals.The
intervalargument indicates the desired coverage probability of the prediction intervals. In this case,intervalis set to[10, 90], which means that the prediction intervals are calculated for the 10th and 90th percentiles, resulting in a theoretical coverage probability of 80%.The
n_bootargument is used to specify the number of bootstrap samples to be used in estimating the prediction intervals. The larger the number of samples, the more accurate the prediction intervals will be, but the longer the calculation will take.
# Backtesting with prediction intervals in test data using in-sample residuals
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(data.loc[:end_validation]),
refit = False
)
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['users'],
exog = data[exog_features],
cv = cv,
metric = 'mean_absolute_error',
interval = [10, 90], # 80% prediction interval
n_boot = 250,
use_in_sample_residuals = True, # Use in-sample residuals
use_binned_residuals = False,
n_jobs = 'auto',
verbose = False,
show_progress = True
)
predictions.head(5)
0%| | 0/45 [00:00<?, ?it/s]
| pred | lower_bound | upper_bound | |
|---|---|---|---|
| 2012-11-16 00:00:00 | 70.009970 | 53.587645 | 85.206036 |
| 2012-11-16 01:00:00 | 45.679914 | 30.385990 | 62.928811 |
| 2012-11-16 02:00:00 | 19.225220 | 2.777457 | 34.043910 |
| 2012-11-16 03:00:00 | -0.039409 | -15.202064 | 15.646154 |
| 2012-11-16 04:00:00 | 0.154831 | -14.950966 | 15.733683 |
# Function to calculate coverage of a given interval
# ======================================================================================
def empirical_coverage(y, lower_bound, upper_bound):
"""
Calculate coverage of a given interval
"""
return np.mean(np.logical_and(y >= lower_bound, y <= upper_bound))
# Plot intervals
# ==============================================================================
plot_prediction_intervals(
predictions = predictions,
y_true = data_test,
target_variable = "users",
initial_x_zoom = ['2012-12-01', '2012-12-20'],
title = "Real value vs predicted in test data",
xaxis_title = "Date time",
yaxis_title = "users",
)
# Predicted interval coverage (on test data)
# ==============================================================================
coverage = empirical_coverage(
y = data.loc[end_validation:, 'users'],
lower_bound = predictions["lower_bound"],
upper_bound = predictions["upper_bound"]
)
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")
# Area of the interval
# ==============================================================================
area = (predictions["upper_bound"] - predictions["lower_bound"]).sum()
print(f"Area of the interval: {round(area, 2)}")
Predicted interval coverage: 62.78 % Area of the interval: 88854.52
The prediction intervals exhibit overconfidence as they tend to be excessively narrow, resulting in a true coverage that falls below the nominal coverage (80 %). This phenomenon arises from the tendency of in-sample residuals to often overestimate the predictive capacity of the model.
Out-sample residuals (non-conditioned on predicted values)¶
To address the issue of overoptimistic intervals, it is possible to use out-sample residuals (residuals from a validation set not seen during training) to estimate the prediction intervals. These residuals can be obtained through backtesting.
# Backtesting on validation data to obtain out-sample residuals
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(data.loc[:end_train]),
refit = False
)
_, predictions_val = backtesting_forecaster(
forecaster = forecaster,
y = data.loc[:end_validation, 'users'],
exog = data.loc[:end_validation, exog_features],
cv = cv,
metric = 'mean_absolute_error',
n_jobs = 'auto',
verbose = False,
show_progress = True
)
0%| | 0/77 [00:00<?, ?it/s]
# Out-sample residuals distribution
# ==============================================================================
residuals = data.loc[predictions_val.index, 'users'] - predictions_val['pred']
print(pd.Series(np.where(residuals < 0, 'negative', 'positive')).value_counts())
plt.rcParams.update({'font.size': 8})
_ = plot_residuals(residuals=residuals, figsize=(7, 4))
positive 1118 negative 730 Name: count, dtype: int64
Then, set_out_sample_residuals() method is used to specify the computed out-sample residuals.
# Store out-sample residuals in the forecaster
# ==============================================================================
forecaster.set_out_sample_residuals(
y_true = data.loc[predictions_val.index, 'users'],
y_pred = predictions_val['pred']
)
Now that the new residuals have been added to the forecaster, the prediction intervals can be calculated using use_in_sample_residuals = False.
# Backtesting with prediction intervals in test data using out-sample residuals
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(data.loc[:end_validation]),
refit = False
)
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['users'],
exog = data[exog_features],
cv = cv,
metric = 'mean_absolute_error',
interval = [10, 90], # 80% prediction interval
n_boot = 250,
use_in_sample_residuals = False, # Use out-sample residuals
use_binned_residuals = False,
n_jobs = 'auto',
verbose = False,
show_progress = True
)
predictions.head(5)
0%| | 0/45 [00:00<?, ?it/s]
| pred | lower_bound | upper_bound | |
|---|---|---|---|
| 2012-11-16 00:00:00 | 70.009970 | 29.697636 | 175.720849 |
| 2012-11-16 01:00:00 | 45.679914 | 4.456010 | 189.808649 |
| 2012-11-16 02:00:00 | 19.225220 | -9.908056 | 179.402612 |
| 2012-11-16 03:00:00 | -0.039409 | -17.221435 | 192.666849 |
| 2012-11-16 04:00:00 | 0.154831 | -31.879388 | 225.809309 |
# Plot intervals
# ==============================================================================
plot_prediction_intervals(
predictions = predictions,
y_true = data_test,
target_variable = "users",
initial_x_zoom = ['2012-12-01', '2012-12-20'],
title = "Real value vs predicted in test data",
xaxis_title = "Date time",
yaxis_title = "users",
)
# Predicted interval coverage (on test data)
# ==============================================================================
coverage = empirical_coverage(
y = data.loc[end_validation:, 'users'],
lower_bound = predictions["lower_bound"],
upper_bound = predictions["upper_bound"]
)
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")
# Area of the interval
# ==============================================================================
area = (predictions["upper_bound"] - predictions["lower_bound"]).sum()
print(f"Area of the interval: {round(area, 2)}")
Predicted interval coverage: 75.37 % Area of the interval: 301725.86
The resulting prediction intervals derived from the out-sample residuals are wider than those generated using the in-sample residuals. This results in an empirical coverage that is closer to the nominal coverage (80 %), although still lower. Examining the plot, it is easy to see that the intervals are particularly wide when the predicted values are low, indicating that the model is not able to properly locate the uncertainty of its predictions.
Intervals conditioned on predicted values (binned residuals)¶
The bootstrapping process assumes that the residuals are independently distributed so that they can be used independently of the predicted value. In reality, this is rarely true; in most cases, the magnitude of the residuals is correlated with the magnitude of the predicted value. In this case, for example, one would hardly expect the error to be the same when the predicted number of users is close to zero as when it is in the hundreds.
To account for the dependence between the residuals and the predicted values, skforecast allows to partition the residuals into K bins, where each bin is associated with a range of predicted values. Using this strategy, the bootstrapping process samples the residuals from different bins depending on the predicted value, which can improve the coverage of the interval while adjusting the width if necessary, allowing the model to better distribute the uncertainty of its predictions.
Internally, skforecast uses a QuantileBinner class to bin data into quantile-based bins using numpy.percentile. This class is similar to KBinsDiscretizer but faster for binning data into quantile-based bins. Bin intervals are defined following the convention: bins[i-1] <= x < bins[i]. The binning process can be adjusted using the argument binner_kwargs of the Forecaster object.
💡 Tip
Since this is a new feature, intervals conditioned on predicted values (binned residuals) are only available for the ForecasterRecursive class. Let us know via GitHub issues if you want us to extend this feature to all Forecasters.
# Create and train forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(random_state=15926, verbose=-1, **params),
lags = lags,
binner_kwargs = {'n_bins': 10}
)
forecaster.fit(
y = data.loc[:end_validation, 'users'],
exog = data.loc[:end_validation, exog_features]
)
During the training process, the forecaster uses the in-sample predictions to define the intervals at which the residuals are stored depending on the predicted value to which they are related (binner_intervals_ attribute).
Although not used in this example, the in-sample residuals are divided into bins and stored in the in_sample_residuals_by_bin_ attribute.
# Intervals of the residual bins
# ==============================================================================
pprint(forecaster.binner_intervals_)
{0.0: (-8.229467171553717, 11.116037535200665),
1.0: (11.116037535200665, 31.879155847370434),
2.0: (31.879155847370434, 75.9019071402224),
3.0: (75.9019071402224, 124.5691653220086),
4.0: (124.5691653220086, 170.35484312260417),
5.0: (170.35484312260417, 218.96823239624555),
6.0: (218.96823239624555, 278.6496576655771),
7.0: (278.6496576655771, 355.13229168292287),
8.0: (355.13229168292287, 486.1660497574729),
9.0: (486.1660497574729, 970.517259284916)}
# Number of in-sample residuals by bin
# ==============================================================================
for k, v in forecaster.in_sample_residuals_by_bin_.items():
print(f"Bin {k}: n={len(v)}")
Bin 0: n=1000 Bin 1: n=1000 Bin 2: n=1000 Bin 3: n=1000 Bin 4: n=1000 Bin 5: n=1000 Bin 6: n=1000 Bin 7: n=1000 Bin 8: n=1000 Bin 9: n=1000
The set_out_sample_residuals() method will bin the residuals according to the intervals learned during fitting. To avoid using too much memory, the number of residuals stored per bin is limited to 10_000 // self.binner.n_bins_. The predictions obtained in the backtesting are used.
# Store out-sample residuals in the forecaster
# ==============================================================================
forecaster.set_out_sample_residuals(
y_true = data.loc[predictions_val.index, 'users'],
y_pred = predictions_val['pred']
)
# Number of out-sample residuals by bin
# ==============================================================================
for k, v in forecaster.out_sample_residuals_by_bin_.items():
print(f"Bin {k}: n={len(v)}")
Bin 0: n=114 Bin 1: n=190 Bin 2: n=183 Bin 3: n=162 Bin 4: n=126 Bin 5: n=164 Bin 6: n=175 Bin 7: n=236 Bin 8: n=232 Bin 9: n=266
# Distribution of the residual by bin
# ==============================================================================
out_sample_residuals_by_bin_df = pd.DataFrame(
dict(
[(k, pd.Series(v))
for k, v in forecaster.out_sample_residuals_by_bin_.items()]
)
)
fig, ax = plt.subplots(figsize=(6, 3))
out_sample_residuals_by_bin_df.boxplot(ax=ax)
ax.set_title("Distribution of residuals by bin", fontsize=12)
ax.set_xlabel("Bin", fontsize=10)
ax.set_ylabel("Residuals", fontsize=10)
plt.show();
The box plots show how the spread and magnitude of the residuals differ depending on the predicted value. For example, for bin 0, whose predicted value is in the interval (-8.2, 11.1), the residuals never exceed an absolute value of 100, while for bin 9, for predicted values in the interval (486.2, 970.5), they often do.
Finally, the prediction intervals for the test data are estimated using the backtesting process, with out-sample residuals conditioned on the predicted values.
# Backtesting with prediction intervals in test data using out-sample residuals
# ==============================================================================
cv = TimeSeriesFold(
steps = 24,
initial_train_size = len(data.loc[:end_validation]),
refit = False
)
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['users'],
exog = data[exog_features],
cv = cv,
metric = 'mean_absolute_error',
interval = [10, 90], # 80% prediction interval
n_boot = 250,
use_in_sample_residuals = False, # Use out-sample residuals
use_binned_residuals = True, # Use binned residuals
n_jobs = 'auto',
verbose = False,
show_progress = True
)
predictions.head(3)
0%| | 0/45 [00:00<?, ?it/s]
| pred | lower_bound | upper_bound | |
|---|---|---|---|
| 2012-11-16 00:00:00 | 70.009970 | 48.514148 | 144.262872 |
| 2012-11-16 01:00:00 | 45.679914 | 19.591406 | 125.205621 |
| 2012-11-16 02:00:00 | 19.225220 | 6.411865 | 76.327318 |
# Plot intervals
# ==============================================================================
plot_prediction_intervals(
predictions = predictions,
y_true = data_test,
target_variable = "users",
initial_x_zoom = ['2012-12-01', '2012-12-20'],
title = "Real value vs predicted in test data",
xaxis_title = "Date time",
yaxis_title = "users",
)
# Predicted interval coverage (on test data)
# ==============================================================================
coverage = empirical_coverage(
y = data.loc[end_validation:, 'users'],
lower_bound = predictions["lower_bound"],
upper_bound = predictions["upper_bound"]
)
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")
# Area of the interval
# ==============================================================================
area = (predictions["upper_bound"] - predictions["lower_bound"]).sum()
print(f"Area of the interval: {round(area, 2)}")
Predicted interval coverage: 84.54 % Area of the interval: 283629.44
When using out-sample residuals conditioned on the predicted value, the area of the interval is significantly reduced and the uncertainty is mainly allocated to the predictions with high values. The empirical coverage is slightly above the expected coverage, which means that the estimated intervals are conservative.
Predict bootstraping, interval, quantile and distribution¶
The previous sections have demonstrated the use of the backtesting process to estimate the prediction interval over a given period of time. The goal is to mimic the behavior of the model in production by running predictions at regular intervals, incrementally updating the input data.
Alternatively, it is possible to run a single prediction that forecasts N steps ahead without going through the entire backtesting process. In such cases, skforecast provides four different methods: predict_bootstrapping, predict_interval, predict_quantile and predict_distribution.
💡 Tip
All of these methods can be used either with in-sample or out-sample residuals using the use_in_sample_residuals argument, and, in the case of the ForecasterRecursive, with binned intervals conditioned on predicted values using the use_binned_residuals argument.
Predict Bootstraping
The predict_bootstrapping method performs the n_boot bootstrapping iterations that generate the alternative prediction paths. These are the underlying values used to compute the intervals, quantiles, and distributions.
# Fit forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
regressor = LGBMRegressor(random_state=15926, verbose=-1, **params),
lags = lags
)
forecaster.fit(
y = data.loc[:end_validation, 'users'],
exog = data.loc[:end_validation, exog_features]
)
# Predict 10 different forecasting sequences of 7 steps each using bootstrapping
# ==============================================================================
boot_predictions = forecaster.predict_bootstrapping(
exog = data_test[exog_features],
steps = 7,
n_boot = 25
)
boot_predictions
| pred_boot_0 | pred_boot_1 | pred_boot_2 | pred_boot_3 | pred_boot_4 | pred_boot_5 | pred_boot_6 | pred_boot_7 | pred_boot_8 | pred_boot_9 | ... | pred_boot_15 | pred_boot_16 | pred_boot_17 | pred_boot_18 | pred_boot_19 | pred_boot_20 | pred_boot_21 | pred_boot_22 | pred_boot_23 | pred_boot_24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2012-11-16 00:00:00 | 81.985520 | 60.377389 | 84.388055 | 69.058073 | 84.363752 | 53.365547 | 62.014035 | 68.985551 | 75.057414 | 67.216612 | ... | 54.514835 | 54.189620 | 36.518993 | 68.557159 | 68.264893 | 70.189381 | 70.991977 | 73.469506 | 85.385037 | 74.674950 |
| 2012-11-16 01:00:00 | 88.671508 | 12.959552 | 46.046186 | 36.611775 | 54.944418 | 37.716277 | 22.194089 | 61.794644 | 44.221255 | 41.234999 | ... | 39.441859 | 34.684937 | 29.390631 | 46.904516 | 49.235859 | 64.798607 | 43.583766 | 36.109031 | 77.169577 | 50.244759 |
| 2012-11-16 02:00:00 | 39.338461 | 24.785275 | 14.884191 | 41.749171 | 25.300967 | 8.741287 | 3.805623 | 43.870139 | 30.912312 | 18.775100 | ... | 16.867980 | 6.233364 | 21.292990 | 16.678047 | 18.935419 | 27.447580 | 21.087522 | 11.084261 | 39.988299 | 6.370777 |
| 2012-11-16 03:00:00 | 19.983940 | -8.053832 | -3.755598 | -9.336178 | -2.473601 | 4.696546 | -4.108438 | 4.013506 | -4.040141 | 5.271591 | ... | -8.488312 | -6.594264 | 3.391765 | -0.488874 | 26.112619 | 7.050683 | -1.361094 | 14.381070 | 14.107233 | -11.178974 |
| 2012-11-16 04:00:00 | 7.359014 | 4.852600 | 3.934356 | 7.529885 | -60.044718 | 1.783976 | -3.470566 | 4.049326 | -8.282527 | 20.979832 | ... | 22.867569 | 3.608031 | 3.891550 | 27.580413 | -30.760255 | -22.188907 | -1.659634 | -1.142344 | 8.388630 | 10.811910 |
| 2012-11-16 05:00:00 | 43.190499 | 49.772787 | 49.603856 | 37.912451 | 14.298424 | 31.803733 | 41.165587 | 17.246246 | 41.555354 | 46.247039 | ... | 70.560448 | 47.767021 | 54.060602 | 34.520989 | 44.763273 | 17.788031 | 25.832253 | 29.960824 | 35.294274 | 37.298048 |
| 2012-11-16 06:00:00 | 109.591869 | 114.900822 | 125.448198 | 100.037473 | 48.076602 | 109.808027 | 138.331594 | 53.236918 | 118.312315 | 107.726050 | ... | 147.752491 | 121.362820 | 138.360903 | 81.182676 | 108.245890 | 53.697026 | 46.161317 | 83.484517 | 72.565764 | 136.768793 |
7 rows × 25 columns
A ridge plot is a useful way to visualize the uncertainty of a forecasting model. This plot estimates a kernel density for each step by using the bootstrapped predictions.
# Ridge plot of bootstrapping predictions
# ==============================================================================
_ = plot_prediction_distribution(boot_predictions, figsize=(7, 4))
Predict Interval
In most cases, the user is interested in a specific interval rather than the entire bootstrapping simulation matrix. To address this need, skforecast provides the predict_interval method. This method internally uses predict_bootstrapping to obtain the bootstrapping matrix and estimates the upper and lower quantiles for each step, thus providing the user with the desired prediction intervals.
# Predict intervals for next 7 steps, quantiles 10th and 90th
# ==============================================================================
predictions = forecaster.predict_interval(
exog = data_test[exog_features],
steps = 7,
interval = [10, 90],
n_boot = 150
)
predictions
| pred | lower_bound | upper_bound | |
|---|---|---|---|
| 2012-11-16 00:00:00 | 70.009970 | 54.107213 | 84.872640 |
| 2012-11-16 01:00:00 | 45.679914 | 28.463273 | 63.218460 |
| 2012-11-16 02:00:00 | 19.225220 | 2.675115 | 37.139233 |
| 2012-11-16 03:00:00 | -0.039409 | -12.239962 | 13.875205 |
| 2012-11-16 04:00:00 | 0.154831 | -16.232195 | 11.242179 |
| 2012-11-16 05:00:00 | 37.330998 | 24.161412 | 55.686697 |
| 2012-11-16 06:00:00 | 116.737843 | 62.052881 | 138.169350 |
Predict Quantile
This method operates identically to predict_interval, with the added feature of enabling users to define a specific list of quantiles for estimation at each step. It's important to remember that these quantiles should be specified within the range of 0 to 1.
# Predict quantiles for next 7 steps, quantiles 5th, 25th, 75th and 95th
# ==============================================================================
predictions = forecaster.predict_quantiles(
exog = data_test[exog_features],
steps = 7,
n_boot = 150,
quantiles = [0.05, 0.25, 0.75, 0.95],
)
predictions
| q_0.05 | q_0.25 | q_0.75 | q_0.95 | |
|---|---|---|---|---|
| 2012-11-16 00:00:00 | 49.305416 | 64.039421 | 76.547694 | 88.905390 |
| 2012-11-16 01:00:00 | 19.299470 | 37.229747 | 53.712462 | 70.768279 |
| 2012-11-16 02:00:00 | -2.806920 | 8.618830 | 29.695881 | 43.638197 |
| 2012-11-16 03:00:00 | -18.082877 | -6.521466 | 7.557586 | 17.076121 |
| 2012-11-16 04:00:00 | -20.856262 | -7.332461 | 5.403864 | 20.607761 |
| 2012-11-16 05:00:00 | 16.475023 | 31.647816 | 47.180808 | 58.337391 |
| 2012-11-16 06:00:00 | 55.484949 | 86.437728 | 128.073968 | 145.109816 |
Predict Distribution
The intervals estimated so far are distribution-free, which means that no assumptions are made about a particular distribution. The predict_dist method in skforecast allows fitting a parametric distribution to the bootstrapped prediction samples obtained with predict_bootstrapping. This is useful when there is reason to believe that the forecast errors follow a particular distribution, such as the normal distribution or the student's t-distribution. The predict_dist method allows the user to specify any continuous distribution from the scipy.stats module.
# Predict the parameters of a normal distribution for the next 7 steps
# ==============================================================================
predictions = forecaster.predict_dist(
exog = data_test[exog_features],
steps = 7,
n_boot = 150,
distribution = norm
)
predictions
| loc | scale | |
|---|---|---|
| 2012-11-16 00:00:00 | 70.273291 | 12.737660 |
| 2012-11-16 01:00:00 | 45.796014 | 14.696426 |
| 2012-11-16 02:00:00 | 18.809760 | 14.545635 |
| 2012-11-16 03:00:00 | 0.504942 | 11.413645 |
| 2012-11-16 04:00:00 | -1.452798 | 12.578119 |
| 2012-11-16 05:00:00 | 38.829072 | 13.605164 |
| 2012-11-16 06:00:00 | 105.823098 | 30.255275 |
Prediction intervals using quantile regression models¶
As opposed to linear regression, which is intended to estimate the conditional mean of the response variable given certain values of the predictor variables, quantile regression aims at estimating the conditional quantiles of the response variable. For a continuous distribution function, the αα-quantile Qα(x)Qα(x) is defined such that the probability of YY being smaller than Qα(x)Qα(x) is, for a given X=xX=x, equal to αα. For example, 36% of the population values are lower than the quantile Q=0.36Q=0.36. The most known quantile is the 50%-quantile, more commonly called the median.
By combining the predictions of two quantile regressors, it is possible to build an interval. Each model estimates one of the limits of the interval. For example, the models obtained for Q=0.1Q=0.1 and Q=0.9Q=0.9 produce an 80% prediction interval (90% - 10% = 80%).
Several machine learning algorithms are capable of modeling quantiles. Some of them are:
Just as the squared-error loss function is used to train models that predict the mean value, a specific loss function is needed in order to train models that predict quantiles. The most common metric used for quantile regression is calles quantile loss or pinball loss:
pinball(y,ˆy)=1nsamplesnsamples−1∑i=0αmax(yi−ˆyi,0)+(1−α)max(ˆyi−yi,0)pinball(y,^y)=1nsamplesnsamples−1∑i=0αmax(yi−^yi,0)+(1−α)max(^yi−yi,0)
where αα is the target quantile, yy the real value and ˆy^y the quantile prediction.
It can be seen that loss differs depending on the evaluated quantile. The higher the quantile, the more the loss function penalizes underestimates, and the less it penalizes overestimates. As with MSE and MAE, the goal is to minimize its values (the lower loss, the better).
Two disadvantages of quantile regression, compared to the bootstrap approach to prediction intervals, are that each quantile needs its regressor and quantile regression is not available for all types of regression models. However, once the models are trained, the inference is much faster since no iterative process is needed.
This type of prediction intervals can be easily estimated using ForecasterDirect and ForecasterDirectMultiVariate models.
⚠ Warning
Forecasters of type ForecasterDirect are slower than ForecasterRecursive because they require training one model per step. Although they can achieve better performance, their scalability is an important limitation when many steps need to be predicted. To limit the time required to run the following examples, the data is aggregated from hourly frequency to daily frequency and only 7 steps ahead (one week) are predicted.
# Data download
# ==============================================================================
data = fetch_dataset(name='vic_electricity')
vic_electricity --------------- Half-hourly electricity demand for Victoria, Australia O'Hara-Wild M, Hyndman R, Wang E, Godahewa R (2022).tsibbledata: Diverse Datasets for 'tsibble'. https://tsibbledata.tidyverts.org/, https://github.com/tidyverts/tsibbledata/. https://tsibbledata.tidyverts.org/reference/vic_elec.html Shape of the dataset: (52608, 4)
# Data preparation (aggregation at daily level)
# ==============================================================================
data = data.resample(rule="D", closed="left", label="right").agg(
{"Demand": "sum", "Temperature": "mean", "Holiday": "max"}
)
data.head(3)
| Demand | Temperature | Holiday | |
|---|---|---|---|
| Time | |||
| 2012-01-01 | 82531.745918 | 21.047727 | True |
| 2012-01-02 | 227778.257304 | 26.578125 | True |
| 2012-01-03 | 275490.988882 | 31.751042 | True |
# Split data into train-validation-test
# ==============================================================================
data = data.loc['2012-01-01 00:00:00': '2014-12-30 23:00:00']
end_train = '2013-12-31 23:59:00'
end_validation = '2014-9-30 23:59:00'
data_train = data.loc[: end_train, :].copy()
data_val = data.loc[end_train:end_validation, :].copy()
data_test = data.loc[end_validation:, :].copy()
print(
f"Train dates : {data_train.index.min()} --- {data_train.index.max()}"
f" (n={len(data_train)})"
)
print(
f"Validation dates : {data_val.index.min()} --- {data_val.index.max()}"
f" (n={len(data_val)})"
)
print(
f"Test dates : {data_test.index.min()} --- {data_test.index.max()}"
f" (n={len(data_test)})"
)
Train dates : 2012-01-01 00:00:00 --- 2013-12-31 00:00:00 (n=731) Validation dates : 2014-01-01 00:00:00 --- 2014-09-30 00:00:00 (n=273) Test dates : 2014-10-01 00:00:00 --- 2014-12-30 00:00:00 (n=91)
# Plot time series partition
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3))
data_train['Demand'].plot(label='train', ax=ax)
data_val['Demand'].plot(label='validation', ax=ax)
data_test['Demand'].plot(label='test', ax=ax)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_ylim(bottom=160_000)
ax.set_ylabel('MW')
ax.set_xlabel('')
ax.set_title('Energy demand')
ax.legend();
Quantile regresion models¶
An 80% prediction interval is estimated for 7 steps-ahead predictions using quantile regression. A LightGBM gradient boosting model is trained in this example, however, the reader may use any other model just replacing the definition of the regressor.
# Create forecasters: one for each bound of the interval
# ==============================================================================
# The forecasters obtained for alpha=0.1 and alpha=0.9 produce a 80% confidence
# interval (90% - 10% = 80%).
# Forecaster for quantile 10%
forecaster_q10 = ForecasterDirect(
regressor = LGBMRegressor(
objective = 'quantile',
metric = 'quantile',
alpha = 0.1,
learning_rate = 0.01,
max_depth = 3,
n_estimators = 500,
verbose = -1
),
lags = 7,
steps = 7
)
# Forecaster for quantile 90%
forecaster_q90 = ForecasterDirect(
regressor = LGBMRegressor(
objective = 'quantile',
metric = 'quantile',
alpha = 0.9,
learning_rate = 0.1,
max_depth = 3,
n_estimators = 100,
verbose = -1
),
lags = 7,
steps = 7
)
forecaster_q10.fit(y=data['Demand'])
forecaster_q90.fit(y=data['Demand'])
When validating a quantile regression model, a custom metric must be provided depending on the quantile being estimated.
# Loss function for each quantile (pinball_loss)
# ==============================================================================
def mean_pinball_loss_q10(y_true, y_pred):
"""
Pinball loss for quantile 10.
"""
return mean_pinball_loss(y_true, y_pred, alpha=0.1)
def mean_pinball_loss_q90(y_true, y_pred):
"""
Pinball loss for quantile 90.
"""
return mean_pinball_loss(y_true, y_pred, alpha=0.9)
Predictions (backtesting)¶
Once the quantile forecasters are trained, they can be used to predict each of the bounds of the forecasting interval.
# Backtesting on test data
# ==============================================================================
cv = TimeSeriesFold(
steps = 7,
initial_train_size = len(data.loc[:end_validation]),
refit = False
)
metric_q10, predictions_q10 = backtesting_forecaster(
forecaster = forecaster_q10,
y = data['Demand'],
cv = cv,
metric = mean_pinball_loss_q10,
n_jobs = 'auto',
verbose = False,
show_progress = True
)
metric_q90, predictions_q90 = backtesting_forecaster(
forecaster = forecaster_q90,
y = data['Demand'],
cv = cv,
metric = mean_pinball_loss_q90,
n_jobs = 'auto',
verbose = False,
show_progress = True
)
0%| | 0/13 [00:00<?, ?it/s]
0%| | 0/13 [00:00<?, ?it/s]
# Plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3))
data.loc[end_validation:, 'Demand'].plot(ax=ax, label='Real value')
ax.fill_between(
data.loc[end_validation:].index,
predictions_q10['pred'],
predictions_q90['pred'],
color = '#444444',
alpha = 0.3,
)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_ylabel('MW')
ax.set_xlabel('')
ax.set_title('Energy demand forecast')
ax.legend();
Predictions generated for each model are used to define the upper and lower limits of the interval.
# Predicted interval coverage (on test data)
# ==============================================================================
coverage = empirical_coverage(
y = data.loc[end_validation:, 'Demand'],
lower_bound = predictions_q10["pred"],
upper_bound = predictions_q90["pred"]
)
print(f"Predicted interval coverage: {round(100 * coverage, 2)} %")
# Area of the interval
# ==============================================================================
area = (predictions_q90["pred"] - predictions_q10["pred"]).sum()
print(f"Area of the interval: {round(area, 2)}")
Predicted interval coverage: 74.73 % Area of the interval: 2832564.24