Exogenous variables (features)¶

Exogenous variables are predictors that are independent of the model being used for forecasting, and their future values must be known in order to include them in the prediction process. The inclusion of exogenous variables can enhance the accuracy of forecasts.

In skforecast, exogenous variables can be easily included as predictors in all forecasting models. To ensure that their effects are accurately accounted for, it is crucial to include these variables during both the training and prediction phases. This will help to optimize the accuracy of forecasts and provide more reliable predictions.

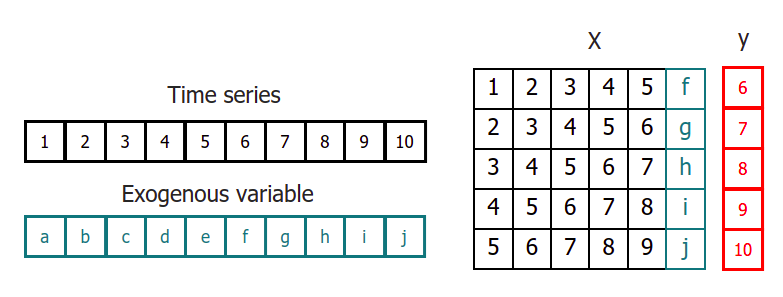
Time series transformation including an exogenous variable.

⚠ Warning

When exogenous variables are included in a forecasting model, it is assumed that all exogenous inputs are known in the future. Do not include exogenous variables as predictors if their future value will not be known when making predictions.

✎ Note

For a detailed guide on how to include categorical exogenous variables, please visit Categorical Features.

Libraries and data¶

In [2]:

# Libraries
# ==============================================================================
import pandas as pd
import matplotlib.pyplot as plt
from lightgbm import LGBMRegressor
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import make_pipeline
from feature_engine.timeseries.forecasting import WindowFeatures
from feature_engine.timeseries.forecasting import LagFeatures
from skforecast.datasets import fetch_dataset
from skforecast.recursive import ForecasterRecursive

# Libraries # ============================================================================== import pandas as pd import matplotlib.pyplot as plt from lightgbm import LGBMRegressor from sklearn.metrics import mean_squared_error from sklearn.pipeline import make_pipeline from feature_engine.timeseries.forecasting import WindowFeatures from feature_engine.timeseries.forecasting import LagFeatures from skforecast.datasets import fetch_dataset from skforecast.recursive import ForecasterRecursive

In [3]:

# Download data
# ==============================================================================
data = fetch_dataset(name='h2o_exog', raw=False)
data.index.name = 'datetime'

# Plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3.5))
data.plot(ax=ax)
plt.show()

# Download data # ============================================================================== data = fetch_dataset(name='h2o_exog', raw=False) data.index.name = 'datetime' # Plot # ============================================================================== fig, ax = plt.subplots(figsize=(7, 3.5)) data.plot(ax=ax) plt.show()

h2o_exog
--------
Monthly expenditure ($AUD) on corticosteroid drugs that the Australian health
system had between 1991 and 2008. Two additional variables (exog_1, exog_2) are
simulated.
Hyndman R (2023). fpp3: Data for Forecasting: Principles and Practice (3rd
Edition). http://pkg.robjhyndman.com/fpp3package/,
https://github.com/robjhyndman/fpp3package, http://OTexts.com/fpp3.
Shape of the dataset: (195, 3)

In [4]:

# Split data in train and test
# ==============================================================================
steps = 36
data_train = data.iloc[:-steps, :]
data_test  = data.iloc[-steps:, :]

# Split data in train and test # ============================================================================== steps = 36 data_train = data.iloc[:-steps, :] data_test = data.iloc[-steps:, :]

Train forecaster with exogenous variables¶

In [5]:

# Create and fit forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
                 regressor = LGBMRegressor(random_state=123, verbose=-1),
                 lags      = 15
             )

forecaster.fit(
    y    = data_train['y'],
    exog = data_train[['exog_1', 'exog_2']]
)

forecaster

# Create and fit forecaster # ============================================================================== forecaster = ForecasterRecursive( regressor = LGBMRegressor(random_state=123, verbose=-1), lags = 15 ) forecaster.fit( y = data_train['y'], exog = data_train[['exog_1', 'exog_2']] ) forecaster

Out[5]:

ForecasterRecursive

General Information

• Regressor: LGBMRegressor
• Lags: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15]
• Window features: None
• Window size: 15
• Exogenous included: True
• Weight function included: False
• Differentiation order: None
• Creation date: 2024-11-21 12:09:07
• Last fit date: 2024-11-21 12:09:08
• Skforecast version: 0.14.0
• Python version: 3.12.4
• Forecaster id: None

Exogenous Variables

exog_1, exog_2

Data Transformations

• Transformer for y: None
• Transformer for exog: None

Training Information

• Training range: [Timestamp('1992-04-01 00:00:00'), Timestamp('2005-06-01 00:00:00')]
• Training index type: DatetimeIndex
• Training index frequency: MS

Regressor Parameters

{'boosting_type': 'gbdt', 'class_weight': None, 'colsample_bytree': 1.0, 'importance_type': 'split', 'learning_rate': 0.1, 'max_depth': -1, 'min_child_samples': 20, 'min_child_weight': 0.001, 'min_split_gain': 0.0, 'n_estimators': 100, 'n_jobs': None, 'num_leaves': 31, 'objective': None, 'random_state': 123, 'reg_alpha': 0.0, 'reg_lambda': 0.0, 'subsample': 1.0, 'subsample_for_bin': 200000, 'subsample_freq': 0, 'verbose': -1}

Fit Kwargs

{}

🛈 API Reference    🗎 User Guide

Prediction¶

If the Forecaster has been trained using exogenous variables, they should be provided during the prediction phase.

In [6]:

# Predict
# ==============================================================================
predictions = forecaster.predict(
                  steps = 36,
                  exog  = data_test[['exog_1', 'exog_2']]
              )

predictions.head(3)

# Predict # ============================================================================== predictions = forecaster.predict( steps = 36, exog = data_test[['exog_1', 'exog_2']] ) predictions.head(3)

Out[6]:

2005-07-01    1.023969
2005-08-01    1.044023
2005-09-01    1.110078
Freq: MS, Name: pred, dtype: float64

In [7]:

# Plot predictions
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3.5))
data_train['y'].plot(ax=ax, label='train')
data_test['y'].plot(ax=ax, label='test')
predictions.plot(ax=ax, label='predictions')
ax.legend()
plt.show()

# Plot predictions # ============================================================================== fig, ax = plt.subplots(figsize=(7, 3.5)) data_train['y'].plot(ax=ax, label='train') data_test['y'].plot(ax=ax, label='test') predictions.plot(ax=ax, label='predictions') ax.legend() plt.show()

In [8]:

# Prediction error
# ==============================================================================
error_mse = mean_squared_error(
                y_true = data_test['y'],
                y_pred = predictions
            )

print(f"Test error (MSE): {error_mse}")

# Prediction error # ============================================================================== error_mse = mean_squared_error( y_true = data_test['y'], y_pred = predictions ) print(f"Test error (MSE): {error_mse}")

Test error (MSE): 0.005576949968874203

Feature importances¶

If exogenous variables are included as predictors, they have a value of feature importances.

In [9]:

# Feature importances with exogenous variables
# ==============================================================================
forecaster.get_feature_importances()

# Feature importances with exogenous variables # ============================================================================== forecaster.get_feature_importances()

Out[9]:

	feature	importance
11	lag_12	66
15	exog_1	49
16	exog_2	37
10	lag_11	36
5	lag_6	31
13	lag_14	26
4	lag_5	26
2	lag_3	25
14	lag_15	24
12	lag_13	23
3	lag_4	23
1	lag_2	22
9	lag_10	18
0	lag_1	16
7	lag_8	16
6	lag_7	15
8	lag_9	12

Handling missing exogenous data in initial training periods¶

When working with time series models that incorporate exogenous variables, it’s common to encounter cases where exogenous data isn't available for the very first part of the historical dataset. This can raise concerns, especially since these initial observations are essential for creating predictors and training matrices. However, full alignment between the exogenous variables and the time series data is only necessary after this initial window period.

In practical terms, this means that if you have missing exogenous values in the early part of your data, they won't prevent model training as long as your exogenous variables are aligned from the point where predictors are created (after the first window_size observations).

In [10]:

# Window required by the Forecaster to create predictors
# ==============================================================================
window_size = forecaster.window_size
print("Window size required by the Forecaster:", window_size)

# Window required by the Forecaster to create predictors # ============================================================================== window_size = forecaster.window_size print("Window size required by the Forecaster:", window_size)

Window size required by the Forecaster: 15

A exogenous variable which skips the first window_size observations of the time series is simulated.

In [11]:

# Simulate data
# ==============================================================================
exog_no_first_window_size = data_train[['exog_1', 'exog_2']].copy()
exog_no_first_window_size = exog_no_first_window_size.iloc[window_size:, :]

# Plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3.5))
data_train[['y']].plot(ax=ax)
exog_no_first_window_size.plot(ax=ax)
plt.show()

# Simulate data # ============================================================================== exog_no_first_window_size = data_train[['exog_1', 'exog_2']].copy() exog_no_first_window_size = exog_no_first_window_size.iloc[window_size:, :] # Plot # ============================================================================== fig, ax = plt.subplots(figsize=(7, 3.5)) data_train[['y']].plot(ax=ax) exog_no_first_window_size.plot(ax=ax) plt.show()

In [12]:

# Create and fit forecaster
# ==============================================================================
forecaster = ForecasterRecursive(
                 regressor = LGBMRegressor(random_state=123, verbose=-1),
                 lags      = 15
             )

forecaster.fit(
    y    = data_train['y'],
    exog = exog_no_first_window_size[['exog_1', 'exog_2']]
)

# Predict
# ==============================================================================
predictions = forecaster.predict(
                  steps = 36,
                  exog  = data_test[['exog_1', 'exog_2']]
              )
predictions.head(3)

# Create and fit forecaster # ============================================================================== forecaster = ForecasterRecursive( regressor = LGBMRegressor(random_state=123, verbose=-1), lags = 15 ) forecaster.fit( y = data_train['y'], exog = exog_no_first_window_size[['exog_1', 'exog_2']] ) # Predict # ============================================================================== predictions = forecaster.predict( steps = 36, exog = data_test[['exog_1', 'exog_2']] ) predictions.head(3)

Out[12]:

2005-07-01    1.023969
2005-08-01    1.044023
2005-09-01    1.110078
Freq: MS, Name: pred, dtype: float64

In [13]:

# Prediction error
# ==============================================================================
error_mse = mean_squared_error(
                y_true = data_test['y'],
                y_pred = predictions
            )

print(f"Test error (MSE): {error_mse}")

# Prediction error # ============================================================================== error_mse = mean_squared_error( y_true = data_test['y'], y_pred = predictions ) print(f"Test error (MSE): {error_mse}")

Test error (MSE): 0.005576949968874203

Since the training matrices are the same as those used with the full exogenous variables, the resulting model is the same and the predictions are identical.

In [14]:

# Check training matrices are the same with both methods
# ==============================================================================
forecaster = ForecasterRecursive(
                 regressor = LGBMRegressor(random_state=123, verbose=-1),
                 lags      = 15
             )

X_train_full_exog, y_train_full_exog = forecaster.create_train_X_y(
    y    = data_train['y'],
    exog = data_train[['exog_1', 'exog_2']]
)

X_train_no_full_exog, y_train_no_full_exog = forecaster.create_train_X_y(
    y    = data_train['y'],
    exog = exog_no_first_window_size[['exog_1', 'exog_2']]
)

pd.testing.assert_frame_equal(X_train_full_exog, X_train_no_full_exog)
pd.testing.assert_series_equal(y_train_full_exog, y_train_no_full_exog)

# Check training matrices are the same with both methods # ============================================================================== forecaster = ForecasterRecursive( regressor = LGBMRegressor(random_state=123, verbose=-1), lags = 15 ) X_train_full_exog, y_train_full_exog = forecaster.create_train_X_y( y = data_train['y'], exog = data_train[['exog_1', 'exog_2']] ) X_train_no_full_exog, y_train_no_full_exog = forecaster.create_train_X_y( y = data_train['y'], exog = exog_no_first_window_size[['exog_1', 'exog_2']] ) pd.testing.assert_frame_equal(X_train_full_exog, X_train_no_full_exog) pd.testing.assert_series_equal(y_train_full_exog, y_train_no_full_exog)

Lagged values and window features from exogenous variables¶

⚠ Warning

This section focuses on lagged values and window features derived from past values of the exogenous variables. These features are different from the window features derived from series being forecasted. See the Window and custom features for more information on the latter.

In [15]:

# Downloading data
# ==============================================================================
data = fetch_dataset(name='bike_sharing', raw=False)
data = data.loc[:, ['users', 'holiday', 'temp', 'windspeed']]
data.head(3)

# Downloading data # ============================================================================== data = fetch_dataset(name='bike_sharing', raw=False) data = data.loc[:, ['users', 'holiday', 'temp', 'windspeed']] data.head(3)

bike_sharing
------------
Hourly usage of the bike share system in the city of Washington D.C. during the
years 2011 and 2012. In addition to the number of users per hour, information
about weather conditions and holidays is available.
Fanaee-T,Hadi. (2013). Bike Sharing Dataset. UCI Machine Learning Repository.
https://doi.org/10.24432/C5W894.
Shape of the dataset: (17544, 11)

Out[15]:

	users	holiday	temp	windspeed
date_time
2011-01-01 00:00:00	16.0	0.0	9.84	0.0
2011-01-01 01:00:00	40.0	0.0	9.02	0.0
2011-01-01 02:00:00	32.0	0.0	9.02	0.0

Combining the LagFeatures and WindowFeatures from feature-engine library, it is straightforward to create lagged values and window features from exogenous variables. In this example, the last 3 lagged values aswell as the mean and standard deviation of the last 24 values are extracted from the exogenous variable temp and windspeed.

In [16]:

# Create lagged features and rolling windows features from exogenous variables
# ==============================================================================
lag_transformer = LagFeatures(
                    variables = ["temp", "windspeed"],
                    periods   = [1, 2, 3],
                  )

wf_transformer = WindowFeatures(
                    variables      = ["temp", "windspeed"],
                    window         = ["24h"],
                    functions      = ["mean"],
                    freq           = "h",
                    missing_values = "ignore",
                    drop_na        = False,
                )

exog_transformer = make_pipeline(
                        wf_transformer,
                        lag_transformer
                   )

exog_transformer

# Create lagged features and rolling windows features from exogenous variables # ============================================================================== lag_transformer = LagFeatures( variables = ["temp", "windspeed"], periods = [1, 2, 3], ) wf_transformer = WindowFeatures( variables = ["temp", "windspeed"], window = ["24h"], functions = ["mean"], freq = "h", missing_values = "ignore", drop_na = False, ) exog_transformer = make_pipeline( wf_transformer, lag_transformer ) exog_transformer

Out[16]:

Pipeline(steps=[('windowfeatures',
                 WindowFeatures(freq='h', functions=['mean'],
                                missing_values='ignore',
                                variables=['temp', 'windspeed'],
                                window=['24h'])),
                ('lagfeatures',
                 LagFeatures(periods=[1, 2, 3],
                             variables=['temp', 'windspeed']))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

In [17]:

data = exog_transformer.fit_transform(data)
data.head(5)

data = exog_transformer.fit_transform(data) data.head(5)

Out[17]:

	users	holiday	temp	windspeed	temp_window_24h_mean	windspeed_window_24h_mean	temp_lag_1	windspeed_lag_1	temp_lag_2	windspeed_lag_2	temp_lag_3	windspeed_lag_3
date_time
2011-01-01 00:00:00	16.0	0.0	9.84	0.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2011-01-01 01:00:00	40.0	0.0	9.02	0.0	9.840000	0.0	9.84	0.0	NaN	NaN	NaN	NaN
2011-01-01 02:00:00	32.0	0.0	9.02	0.0	9.430000	0.0	9.02	0.0	9.84	0.0	NaN	NaN
2011-01-01 03:00:00	13.0	0.0	9.84	0.0	9.293333	0.0	9.02	0.0	9.02	0.0	9.84	0.0
2011-01-01 04:00:00	1.0	0.0	9.84	0.0	9.430000	0.0	9.84	0.0	9.02	0.0	9.02	0.0

Backtesting with exogenous variables¶

All the backtesting strategies available in skforecast can also be applied when incorporating exogenous variables in the forecasting model. Visit the Backtesting section for more information.