Global Forecasting Models: Dependent multi-series forecasting (Multivariate forecasting)¶

Univariate time series forecasting models a single time series as a linear or nonlinear combination of its lags, using past values of the series to predict its future. Global forecasting, involves building a single predictive model that considers all time series simultaneously. It attempts to capture the core patterns that govern the series, thereby mitigating the potential noise that each series might introduce. This approach is computationally efficient, easy to maintain, and can yield more robust generalizations across time series.

In dependent multi-series forecasting (multivariate time series), all series are modeled together in a single model, considering that each time series depends not only on its past values but also on the past values of the other series. The forecaster is expected not only to learn the information of each series separately but also to relate them. An example is the measurements made by all the sensors (flow, temperature, pressure...) installed on an industrial machine such as a compressor.

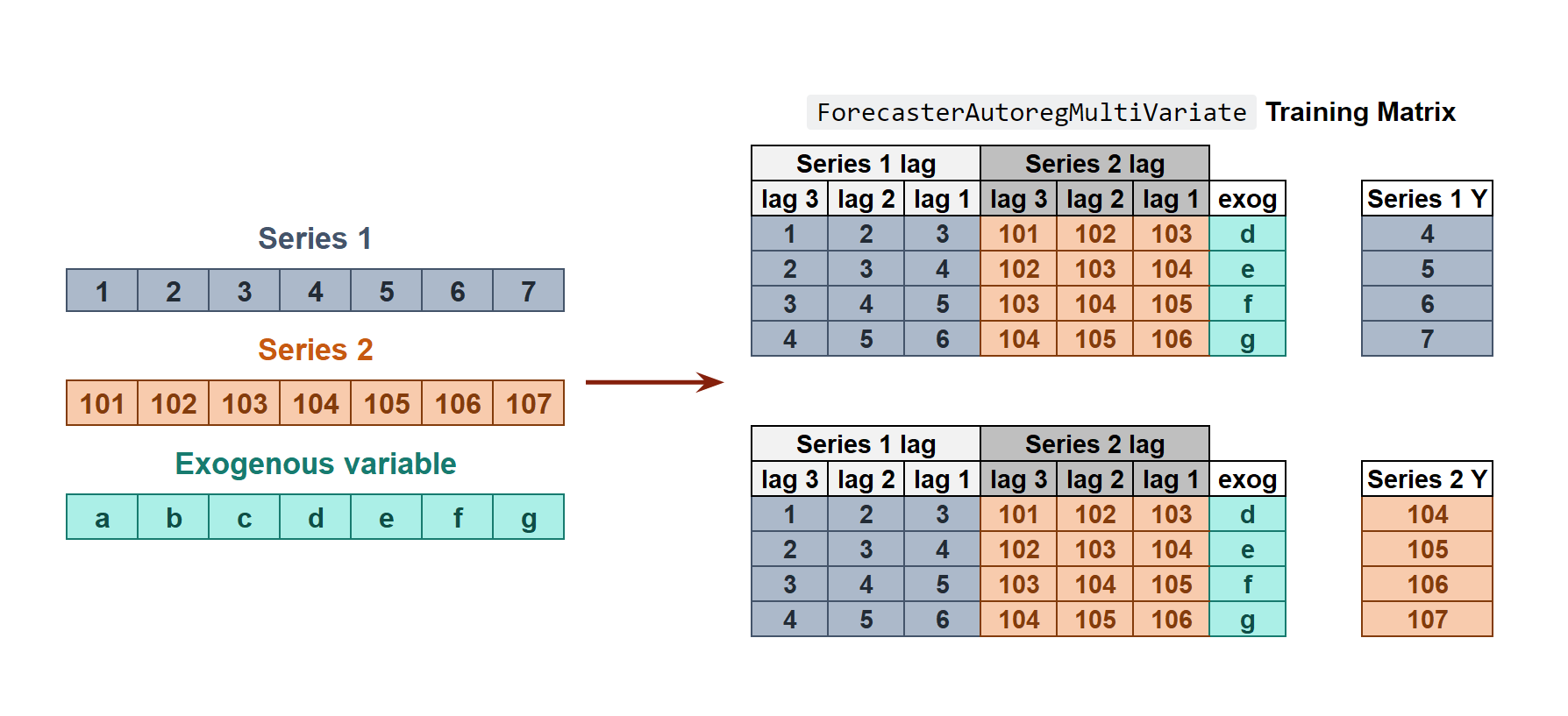
Internal Forecaster time series transformation to train a forecaster with multiple dependent time series.

Since as many training matrices are created as there are series in the dataset, it must be decided on which level the forecasting will be performed. To predict the next n steps a model is trained for each step to be predicted, the selected level in the figure is Series 1. This strategy is of the type direct multi-step forecasting.

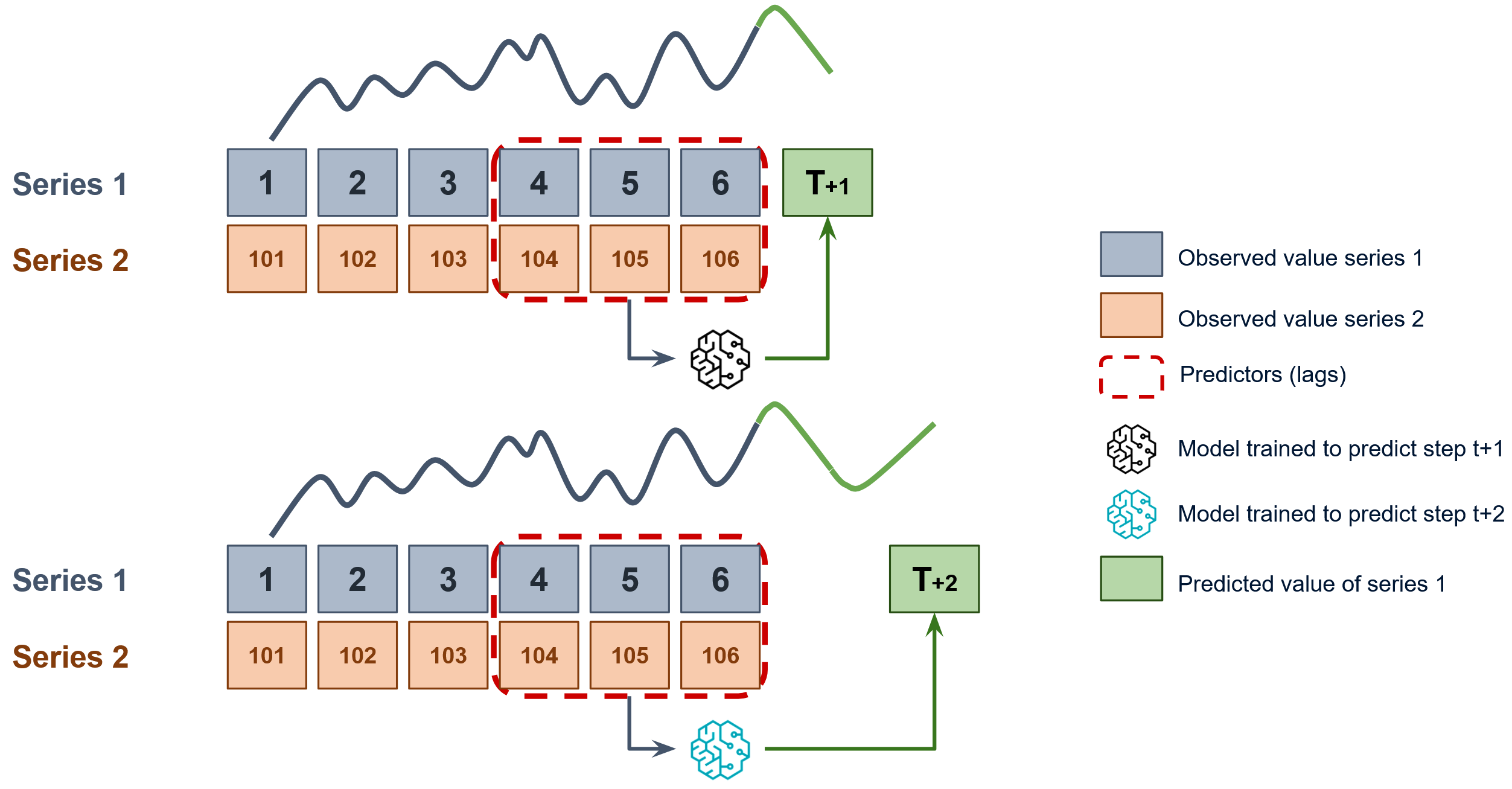
Diagram of direct forecasting with multiple dependent time series.

Using the ForecasterDirectMultiVariate class, it is possible to easily build machine learning models for dependent multi-series forecasting.

✎ Note

Why can only one series be predicted?

The key challenge with directly applying a strategy to multiple time series is scalability. Typically, each time series and each time step would require its own model. For instance, if you have 1,000 time series and a prediction horizon of 24 steps, you would need to train 24,000 separate models. This approach becomes impractical very quickly. That's why the ForecasterDirectMultiVariate can learn from multiple series but can only predict one at a time.

The good news? We are developing a new class that will enable predictions for multiple series simultaneously. Stay tuned!

✎ Note

Skforecast offers additional approaches to create Global Forecasting Models:

• Global Forecasting Models: Independent multi-series forecasting
• Global Forecasting Models: Time series with different lengths and different exogenous variables
• Global Forecasting Models: Forecasting with Deep Learning

To learn more about global forecasting models visit our examples:

• Global Forecasting Models: Multi-series forecasting with Python and skforecast
• Scalable Forecasting: Modeling thousand time series with a single global model
• Global Forecasting Models: Comparative Analysis of Single and Multi-Series Forecasting Modeling
• Forecasting with Deep Learning

Libraries and data¶

In [1]:

# Libraries
# ==============================================================================
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from lightgbm import LGBMRegressor
from sklearn.metrics import mean_absolute_error

from skforecast.datasets import fetch_dataset
from skforecast.preprocessing import RollingFeatures
from skforecast.direct import ForecasterDirectMultiVariate
from skforecast.model_selection import TimeSeriesFold
from skforecast.model_selection import backtesting_forecaster_multiseries
from skforecast.model_selection import grid_search_forecaster_multiseries
from skforecast.model_selection import random_search_forecaster_multiseries
from skforecast.model_selection import bayesian_search_forecaster_multiseries

# Libraries # ============================================================================== import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.preprocessing import StandardScaler from lightgbm import LGBMRegressor from sklearn.metrics import mean_absolute_error from skforecast.datasets import fetch_dataset from skforecast.preprocessing import RollingFeatures from skforecast.direct import ForecasterDirectMultiVariate from skforecast.model_selection import TimeSeriesFold from skforecast.model_selection import backtesting_forecaster_multiseries from skforecast.model_selection import grid_search_forecaster_multiseries from skforecast.model_selection import random_search_forecaster_multiseries from skforecast.model_selection import bayesian_search_forecaster_multiseries

In [2]:

# Data download
# ==============================================================================
data = fetch_dataset(name="air_quality_valencia_no_missing")

# Data download # ============================================================================== data = fetch_dataset(name="air_quality_valencia_no_missing")

air_quality_valencia_no_missing
-------------------------------
Hourly measures of several air chemical pollutant at Valencia city (Avd.
Francia) from 2019-01-01 to 20213-12-31. Including the following variables:
pm2.5 (µg/m³), CO (mg/m³), NO (µg/m³), NO2 (µg/m³), PM10 (µg/m³), NOx (µg/m³),
O3 (µg/m³), Veloc. (m/s), Direc. (degrees), SO2 (µg/m³). Missing values have
been imputed using linear interpolation.
Red de Vigilancia y Control de la Contaminación Atmosférica, 46250047-València -
Av. França, https://mediambient.gva.es/es/web/calidad-ambiental/datos-
historicos.
Shape of the dataset: (43824, 10)

In [3]:

# Aggregate at daily frequency to reduce dimensions
# ==============================================================================
data = data.resample('D').mean()
print("Shape: ", data.shape)
data.head()

# Aggregate at daily frequency to reduce dimensions # ============================================================================== data = data.resample('D').mean() print("Shape: ", data.shape) data.head()

Shape:  (1826, 10)

Out[3]:

	so2	co	no	no2	pm10	nox	o3	veloc.	direc.	pm2.5
datetime
2019-01-01	6.000000	0.141667	17.375000	37.250000	21.458333	63.458333	20.291667	0.416667	207.416667	17.208333
2019-01-02	6.041667	0.170833	23.458333	49.333333	26.416667	85.041667	11.708333	0.579167	225.375000	17.375000
2019-01-03	5.916667	0.216667	41.291667	53.250000	36.166667	116.333333	9.833333	0.500000	211.833333	21.625000
2019-01-04	5.458333	0.204167	21.208333	45.750000	32.208333	77.958333	15.166667	0.675000	199.583333	22.166667
2019-01-05	4.541667	0.191667	10.291667	36.375000	32.875000	51.833333	21.083333	0.875000	254.208333	24.916667

In [4]:

data

data

Out[4]:

	so2	co	no	no2	pm10	nox	o3	veloc.	direc.	pm2.5
datetime
2019-01-01	6.000000	0.141667	17.375000	37.250000	21.458333	63.458333	20.291667	0.416667	207.416667	17.208333
2019-01-02	6.041667	0.170833	23.458333	49.333333	26.416667	85.041667	11.708333	0.579167	225.375000	17.375000
2019-01-03	5.916667	0.216667	41.291667	53.250000	36.166667	116.333333	9.833333	0.500000	211.833333	21.625000
2019-01-04	5.458333	0.204167	21.208333	45.750000	32.208333	77.958333	15.166667	0.675000	199.583333	22.166667
2019-01-05	4.541667	0.191667	10.291667	36.375000	32.875000	51.833333	21.083333	0.875000	254.208333	24.916667
...	...	...	...	...	...	...	...	...	...	...
2023-12-27	3.250000	0.100000	28.250000	58.041667	28.083333	101.291667	14.666667	0.445833	208.958333	18.416667
2023-12-28	3.166667	0.100000	38.708333	56.416667	35.666667	115.666667	15.375000	0.250000	168.208333	22.291667
2023-12-29	3.000000	0.100000	29.979167	55.666667	51.354167	101.458333	8.958333	0.237500	231.458333	37.250000
2023-12-30	3.750000	0.100000	33.458333	56.208333	46.375000	107.333333	12.000000	0.320833	144.916667	36.041667
2023-12-31	3.000000	0.100000	5.500000	20.541667	21.583333	28.791667	42.375000	1.887500	224.750000	14.250000

1826 rows × 10 columns

In [5]:

# Split data into train-val-test
# ==============================================================================
end_train = '2023-05-31 23:59:59'
data_train = data.loc[:end_train, :].copy()
data_test  = data.loc[end_train:, :].copy()

print(
    f"Train dates : {data_train.index.min()} --- {data_train.index.max()}  "
    f"(n={len(data_train)})"
)
print(
    f"Test dates  : {data_test.index.min()} --- {data_test.index.max()}  "
    f"(n={len(data_test)})"
)

# Split data into train-val-test # ============================================================================== end_train = '2023-05-31 23:59:59' data_train = data.loc[:end_train, :].copy() data_test = data.loc[end_train:, :].copy() print( f"Train dates : {data_train.index.min()} --- {data_train.index.max()} " f"(n={len(data_train)})" ) print( f"Test dates : {data_test.index.min()} --- {data_test.index.max()} " f"(n={len(data_test)})" )

Train dates : 2019-01-01 00:00:00 --- 2023-05-31 00:00:00  (n=1612)
Test dates  : 2023-06-01 00:00:00 --- 2023-12-31 00:00:00  (n=214)

In [6]:

# Plot time series
# ==============================================================================
fig, axes = plt.subplots(nrows=3, ncols=1, figsize=(9, 5), sharex=True)

for i, col in enumerate(data.columns[:3]):
    data_train[col].plot(ax=axes[i], label='train')
    data_test[col].plot(ax=axes[i], label='test')
    axes[i].set_ylabel('Concentration (ug/m^3)')
    axes[i].set_title(col)
    axes[i].legend(loc='upper right')

fig.tight_layout()
plt.show();

# Plot time series # ============================================================================== fig, axes = plt.subplots(nrows=3, ncols=1, figsize=(9, 5), sharex=True) for i, col in enumerate(data.columns[:3]): data_train[col].plot(ax=axes[i], label='train') data_test[col].plot(ax=axes[i], label='test') axes[i].set_ylabel('Concentration (ug/m^3)') axes[i].set_title(col) axes[i].legend(loc='upper right') fig.tight_layout() plt.show();

Train and predict ForecasterDirectMultiVariate¶

When initializing the forecaster, the series (level) to be predicted and the maximum number of steps must be indicated since a different model will be created for each step.

✎ Note

ForecasterDirectMultiVariate includes the n_jobs parameter, allowing multi-process parallelization. This allows to train regressors for all steps simultaneously.

The benefits of parallelization depend on several factors, including the regressor used, the number of fits to be performed, and the volume of data involved. When the n_jobs parameter is set to 'auto', the level of parallelization is automatically selected based on heuristic rules that aim to choose the best option for each scenario.

For a more detailed look at parallelization, visit Parallelization in skforecast.

In [7]:

# Create and fit forecaster MultiVariate
# ==============================================================================
forecaster = ForecasterDirectMultiVariate(
                 regressor       = LGBMRegressor(random_state=123, verbose=-1),
                 level           = 'co',
                 steps           = 7,
                 lags            = 7,
                 window_features = RollingFeatures(stats=['mean'], window_sizes=[7]),
                 n_jobs          = 'auto'
             )

forecaster.fit(series=data_train)
forecaster

# Create and fit forecaster MultiVariate # ============================================================================== forecaster = ForecasterDirectMultiVariate( regressor = LGBMRegressor(random_state=123, verbose=-1), level = 'co', steps = 7, lags = 7, window_features = RollingFeatures(stats=['mean'], window_sizes=[7]), n_jobs = 'auto' ) forecaster.fit(series=data_train) forecaster

Out[7]:

ForecasterDirectMultiVariate

General Information

• Regressor: LGBMRegressor
• Target series (level): co
• Lags: [1 2 3 4 5 6 7]
• Window features: ['roll_mean_7']
• Window size: 7
• Maximum steps to predict: 7
• Exogenous included: False
• Weight function included: False
• Differentiation order: None
• Creation date: 2024-11-11 12:11:12
• Last fit date: 2024-11-11 12:11:15
• Skforecast version: 0.14.0
• Python version: 3.11.10
• Forecaster id: None

Exogenous Variables

None

Data Transformations

• Transformer for series: StandardScaler()
• Transformer for exog: None

Training Information

• Target series (level): co
• Multivariate series: so2, co, no, no2, pm10, nox, o3, veloc., direc., pm2.5
• Training range: [Timestamp('2019-01-01 00:00:00'), Timestamp('2023-05-31 00:00:00')]
• Training index type: DatetimeIndex
• Training index frequency: D

Regressor Parameters

{'boosting_type': 'gbdt', 'class_weight': None, 'colsample_bytree': 1.0, 'importance_type': 'split', 'learning_rate': 0.1, 'max_depth': -1, 'min_child_samples': 20, 'min_child_weight': 0.001, 'min_split_gain': 0.0, 'n_estimators': 100, 'n_jobs': None, 'num_leaves': 31, 'objective': None, 'random_state': 123, 'reg_alpha': 0.0, 'reg_lambda': 0.0, 'subsample': 1.0, 'subsample_for_bin': 200000, 'subsample_freq': 0, 'verbose': -1}

Fit Kwargs

{}

🛈 API Reference    🗎 User Guide

When predicting, the value of steps must be less than or equal to the value of steps defined when initializing the forecaster. Starts at 1.

• If int only steps within the range of 1 to int are predicted.

• If list of int. Only the steps contained in the list are predicted.

• If None as many steps are predicted as were defined at initialization.

In [8]:

# Predict with forecaster MultiVariate
# ==============================================================================
predictions = forecaster.predict(steps=None)  # All steps
predictions

# Predict with forecaster MultiVariate # ============================================================================== predictions = forecaster.predict(steps=None) # All steps predictions

Out[8]:

	co
2023-06-01	0.100046
2023-06-02	0.106861
2023-06-03	0.109452
2023-06-04	0.106873
2023-06-05	0.095040
2023-06-06	0.108114
2023-06-07	0.104563

In [9]:

# Predict only a subset of steps
# ==============================================================================
predictions = forecaster.predict(steps=[1, 5])
predictions

# Predict only a subset of steps # ============================================================================== predictions = forecaster.predict(steps=[1, 5]) predictions

Out[9]:

	co
2023-06-01	0.100046
2023-06-05	0.095040

In [10]:

# Predict intervals
# ==============================================================================
predictions = forecaster.predict_interval(random_state=9871)
predictions

# Predict intervals # ============================================================================== predictions = forecaster.predict_interval(random_state=9871) predictions

Out[10]:

	co	co_lower_bound	co_upper_bound
2023-06-01	0.100046	0.089832	0.111817
2023-06-02	0.106861	0.093617	0.116840
2023-06-03	0.109452	0.098173	0.124021
2023-06-04	0.106873	0.092592	0.122083
2023-06-05	0.095040	0.085764	0.107368
2023-06-06	0.108114	0.094295	0.118989
2023-06-07	0.104563	0.092779	0.117915

Backtesting MultiVariate¶

See the backtesting user guide to learn more about backtesting.

In [11]:

# Backtesting MultiVariate
# ==============================================================================
cv = TimeSeriesFold(
         steps                 = 7,
         initial_train_size    = len(data_train),
         refit                 = False,
         allow_incomplete_fold = True
     )

metrics_levels, backtest_predictions = backtesting_forecaster_multiseries(
                                           forecaster    = forecaster,
                                           series        = data,
                                           cv            = cv,
                                           metric        = 'mean_absolute_error',
                                           n_jobs        = 'auto',
                                           verbose       = False,
                                           show_progress = True
                                       )
print("Backtest metrics")
display(metrics_levels)
print("")
print("Backtest predictions")
backtest_predictions.head(4)

# Backtesting MultiVariate # ============================================================================== cv = TimeSeriesFold( steps = 7, initial_train_size = len(data_train), refit = False, allow_incomplete_fold = True ) metrics_levels, backtest_predictions = backtesting_forecaster_multiseries( forecaster = forecaster, series = data, cv = cv, metric = 'mean_absolute_error', n_jobs = 'auto', verbose = False, show_progress = True ) print("Backtest metrics") display(metrics_levels) print("") print("Backtest predictions") backtest_predictions.head(4)

  0%|          | 0/31 [00:00<?, ?it/s]

Backtest metrics

	levels	mean_absolute_error
0	co	0.017541

Backtest predictions

Out[11]:

	co
2023-06-01	0.100046
2023-06-02	0.106861
2023-06-03	0.109452
2023-06-04	0.106873

Hyperparameter tuning and lags selection MultiVariate¶

The grid_search_forecaster_multiseries, random_search_forecaster_multiseries and bayesian_search_forecaster_multiseries functions in the model_selection module allow for lags and hyperparameter optimization. It is performed using the backtesting strategy for validation as in other Forecasters, see the user guide here.

The following example shows how to use random_search_forecaster_multiseries to find the best lags and model hyperparameters.

In [12]:

# Create and forecaster MultiVariate
# ==============================================================================
forecaster = ForecasterDirectMultiVariate(
                 regressor          = LGBMRegressor(random_state=123, verbose=-1),
                 level              = 'co',
                 steps              = 7,
                 lags               = 7,
                 window_features    = RollingFeatures(stats=['mean'], window_sizes=[7]),
                 transformer_series = StandardScaler()
             )

# Create and forecaster MultiVariate # ============================================================================== forecaster = ForecasterDirectMultiVariate( regressor = LGBMRegressor(random_state=123, verbose=-1), level = 'co', steps = 7, lags = 7, window_features = RollingFeatures(stats=['mean'], window_sizes=[7]), transformer_series = StandardScaler() )

In [13]:

# Random search MultiVariate
# ==============================================================================
lags_grid = [7, 14]
param_distributions = {
    'n_estimators': np.arange(start=10, stop=20, step=1, dtype=int),
    'max_depth': np.arange(start=3, stop=6, step=1, dtype=int)
}

cv = TimeSeriesFold(
         steps                 = 7,
         initial_train_size    = len(data_train),
         refit                 = False,
         allow_incomplete_fold = True
     )

results = random_search_forecaster_multiseries(
              forecaster          = forecaster,
              series              = data,
              exog                = None,
              lags_grid           = lags_grid,
              param_distributions = param_distributions,
              cv                  = cv,
              metric              = 'mean_absolute_error',
              aggregate_metric    = 'weighted_average',
              n_iter              = 5,
              return_best         = False,
              n_jobs              = 'auto',
              verbose             = False,
              show_progress       = True
          )

results

# Random search MultiVariate # ============================================================================== lags_grid = [7, 14] param_distributions = { 'n_estimators': np.arange(start=10, stop=20, step=1, dtype=int), 'max_depth': np.arange(start=3, stop=6, step=1, dtype=int) } cv = TimeSeriesFold( steps = 7, initial_train_size = len(data_train), refit = False, allow_incomplete_fold = True ) results = random_search_forecaster_multiseries( forecaster = forecaster, series = data, exog = None, lags_grid = lags_grid, param_distributions = param_distributions, cv = cv, metric = 'mean_absolute_error', aggregate_metric = 'weighted_average', n_iter = 5, return_best = False, n_jobs = 'auto', verbose = False, show_progress = True ) results

lags grid:   0%|          | 0/2 [00:00<?, ?it/s]

params grid:   0%|          | 0/5 [00:00<?, ?it/s]

Out[13]:

	levels	lags	lags_label	params	mean_absolute_error	n_estimators	max_depth
0	[co]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	{'n_estimators': 19, 'max_depth': 5}	0.016567	19	5
1	[co]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	{'n_estimators': 16, 'max_depth': 5}	0.017329	16	5
2	[co]	[1, 2, 3, 4, 5, 6, 7]	[1, 2, 3, 4, 5, 6, 7]	{'n_estimators': 18, 'max_depth': 3}	0.017705	18	3
3	[co]	[1, 2, 3, 4, 5, 6, 7]	[1, 2, 3, 4, 5, 6, 7]	{'n_estimators': 19, 'max_depth': 5}	0.017724	19	5
4	[co]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	{'n_estimators': 18, 'max_depth': 3}	0.017854	18	3
5	[co]	[1, 2, 3, 4, 5, 6, 7]	[1, 2, 3, 4, 5, 6, 7]	{'n_estimators': 17, 'max_depth': 3}	0.017885	17	3
6	[co]	[1, 2, 3, 4, 5, 6, 7]	[1, 2, 3, 4, 5, 6, 7]	{'n_estimators': 16, 'max_depth': 5}	0.017923	16	5
7	[co]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	{'n_estimators': 15, 'max_depth': 3}	0.018076	15	3
8	[co]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	{'n_estimators': 17, 'max_depth': 3}	0.018101	17	3
9	[co]	[1, 2, 3, 4, 5, 6, 7]	[1, 2, 3, 4, 5, 6, 7]	{'n_estimators': 15, 'max_depth': 3}	0.018235	15	3

It is also possible to perform a bayesian optimization with optuna using the bayesian_search_forecaster_multiseries function. For more information about this type of optimization, see the user guide here.

In [14]:

# Bayesian search hyperparameters and lags with Optuna
# ==============================================================================
forecaster = ForecasterDirectMultiVariate(
                 regressor       = LGBMRegressor(random_state=123, verbose=-1),
                 level           = 'co',
                 steps           = 7,
                 lags            = 7,
                 window_features = RollingFeatures(stats=['mean'], window_sizes=[7])
             )

# Search space
def search_space(trial):
    search_space  = {
        'lags'            : trial.suggest_categorical('lags', [7, 14]),
        'n_estimators'    : trial.suggest_int('n_estimators', 10, 20),
        'min_samples_leaf': trial.suggest_int('min_samples_leaf', 1., 10),
        'max_features'    : trial.suggest_categorical('max_features', ['log2', 'sqrt'])
    }

    return search_space

cv = TimeSeriesFold(
         steps                 = 7,
         initial_train_size    = len(data_train),
         refit                 = False,
         allow_incomplete_fold = True
     )

results, best_trial = bayesian_search_forecaster_multiseries(
                          forecaster            = forecaster,
                          series                = data,
                          exog                  = None, 
                          search_space          = search_space,
                          cv                    = cv,
                          metric                = 'mean_absolute_error',
                          aggregate_metric      = 'weighted_average',
                          n_trials              = 5,
                          random_state          = 123,
                          return_best           = False,
                          n_jobs                = 'auto',
                          verbose               = False,
                          show_progress         = True,
                          kwargs_create_study   = {},
                          kwargs_study_optimize = {}
                      )

results.head(4)

# Bayesian search hyperparameters and lags with Optuna # ============================================================================== forecaster = ForecasterDirectMultiVariate( regressor = LGBMRegressor(random_state=123, verbose=-1), level = 'co', steps = 7, lags = 7, window_features = RollingFeatures(stats=['mean'], window_sizes=[7]) ) # Search space def search_space(trial): search_space = { 'lags' : trial.suggest_categorical('lags', [7, 14]), 'n_estimators' : trial.suggest_int('n_estimators', 10, 20), 'min_samples_leaf': trial.suggest_int('min_samples_leaf', 1., 10), 'max_features' : trial.suggest_categorical('max_features', ['log2', 'sqrt']) } return search_space cv = TimeSeriesFold( steps = 7, initial_train_size = len(data_train), refit = False, allow_incomplete_fold = True ) results, best_trial = bayesian_search_forecaster_multiseries( forecaster = forecaster, series = data, exog = None, search_space = search_space, cv = cv, metric = 'mean_absolute_error', aggregate_metric = 'weighted_average', n_trials = 5, random_state = 123, return_best = False, n_jobs = 'auto', verbose = False, show_progress = True, kwargs_create_study = {}, kwargs_study_optimize = {} ) results.head(4)

  0%|          | 0/5 [00:00<?, ?it/s]

Out[14]:

	levels	lags	params	mean_absolute_error	n_estimators	min_samples_leaf	max_features
0	[co]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	{'n_estimators': 16, 'min_samples_leaf': 9, 'm...	0.018025	16	9	log2
1	[co]	[1, 2, 3, 4, 5, 6, 7]	{'n_estimators': 14, 'min_samples_leaf': 8, 'm...	0.019328	14	8	log2
2	[co]	[1, 2, 3, 4, 5, 6, 7]	{'n_estimators': 15, 'min_samples_leaf': 4, 'm...	0.020233	15	4	sqrt
3	[co]	[1, 2, 3, 4, 5, 6, 7]	{'n_estimators': 12, 'min_samples_leaf': 6, 'm...	0.020452	12	6	log2

best_trial contains information of the trial which achived the best results. See more in Study class.

In [15]:

# Optuna best trial in the study
# ==============================================================================
best_trial

# Optuna best trial in the study # ============================================================================== best_trial

Out[15]:

FrozenTrial(number=3, state=1, values=[0.018024662716443113], datetime_start=datetime.datetime(2024, 11, 11, 12, 11, 27, 31959), datetime_complete=datetime.datetime(2024, 11, 11, 12, 11, 28, 127266), params={'lags': 14, 'n_estimators': 16, 'min_samples_leaf': 9, 'max_features': 'log2'}, user_attrs={}, system_attrs={}, intermediate_values={}, distributions={'lags': CategoricalDistribution(choices=(7, 14)), 'n_estimators': IntDistribution(high=20, log=False, low=10, step=1), 'min_samples_leaf': IntDistribution(high=10, log=False, low=1, step=1), 'max_features': CategoricalDistribution(choices=('log2', 'sqrt'))}, trial_id=3, value=None)

Different lags for each time series¶

If a dict is passed to the lags argument, it allows setting different lags for each of the series. The keys of the dictionary must be the names of the series to be used during training.

In [16]:

data

data

Out[16]:

	so2	co	no	no2	pm10	nox	o3	veloc.	direc.	pm2.5
datetime
2019-01-01	6.000000	0.141667	17.375000	37.250000	21.458333	63.458333	20.291667	0.416667	207.416667	17.208333
2019-01-02	6.041667	0.170833	23.458333	49.333333	26.416667	85.041667	11.708333	0.579167	225.375000	17.375000
2019-01-03	5.916667	0.216667	41.291667	53.250000	36.166667	116.333333	9.833333	0.500000	211.833333	21.625000
2019-01-04	5.458333	0.204167	21.208333	45.750000	32.208333	77.958333	15.166667	0.675000	199.583333	22.166667
2019-01-05	4.541667	0.191667	10.291667	36.375000	32.875000	51.833333	21.083333	0.875000	254.208333	24.916667
...	...	...	...	...	...	...	...	...	...	...
2023-12-27	3.250000	0.100000	28.250000	58.041667	28.083333	101.291667	14.666667	0.445833	208.958333	18.416667
2023-12-28	3.166667	0.100000	38.708333	56.416667	35.666667	115.666667	15.375000	0.250000	168.208333	22.291667
2023-12-29	3.000000	0.100000	29.979167	55.666667	51.354167	101.458333	8.958333	0.237500	231.458333	37.250000
2023-12-30	3.750000	0.100000	33.458333	56.208333	46.375000	107.333333	12.000000	0.320833	144.916667	36.041667
2023-12-31	3.000000	0.100000	5.500000	20.541667	21.583333	28.791667	42.375000	1.887500	224.750000	14.250000

1826 rows × 10 columns

In [17]:

data.columns

data.columns

Out[17]:

Index(['so2', 'co', 'no', 'no2', 'pm10', 'nox', 'o3', 'veloc.', 'direc.',
       'pm2.5'],
      dtype='object')

In [18]:

# Create and fit forecaster MultiVariate Custom lags
# ==============================================================================
lags_dict = {
    'so2': [7, 14], 'co': 7, 'no': [7, 14], 'no2': [7, 14],
    'pm10': [7, 14], 'nox': [7, 14], 'o3': [7, 14], 'veloc.': 3,
    'direc.': 3, 'pm2.5': [7, 14]
}
forecaster = ForecasterDirectMultiVariate(
                 regressor          = LGBMRegressor(random_state=123, verbose=-1),
                 level              = 'co',
                 steps              = 7,
                 lags               = lags_dict,
                 transformer_series = StandardScaler(),
                 transformer_exog   = None,
                 weight_func        = None
             )

forecaster.fit(series=data_train)

# Predict
# ==============================================================================
predictions = forecaster.predict(steps=7)
display(predictions)

# Create and fit forecaster MultiVariate Custom lags # ============================================================================== lags_dict = { 'so2': [7, 14], 'co': 7, 'no': [7, 14], 'no2': [7, 14], 'pm10': [7, 14], 'nox': [7, 14], 'o3': [7, 14], 'veloc.': 3, 'direc.': 3, 'pm2.5': [7, 14] } forecaster = ForecasterDirectMultiVariate( regressor = LGBMRegressor(random_state=123, verbose=-1), level = 'co', steps = 7, lags = lags_dict, transformer_series = StandardScaler(), transformer_exog = None, weight_func = None ) forecaster.fit(series=data_train) # Predict # ============================================================================== predictions = forecaster.predict(steps=7) display(predictions)

	co
2023-06-01	0.098798
2023-06-02	0.107185
2023-06-03	0.112225
2023-06-04	0.107208
2023-06-05	0.098643
2023-06-06	0.100375
2023-06-07	0.099513

If a None is passed to any of the keys of the lags argument, that series will not be used to create the X training matrix.

In this example, no lags are created for the 'co' series, but since it is the level of the forecaster, the 'co' column will be used to create the y training matrix.

In [19]:

# Create and fit forecaster MultiVariate Custom lags with None
# ==============================================================================
lags_dict = {
    'so2': [7, 14], 'co': None, 'no': [7, 14], 'no2': [7, 14],
    'pm10': [7, 14], 'nox': [7, 14], 'o3': [7, 14], 'veloc.': 3,
    'direc.': 3, 'pm2.5': [7, 14]
}
forecaster = ForecasterDirectMultiVariate(
                 regressor          = LGBMRegressor(random_state=123, verbose=-1),
                 level              = 'co',
                 lags               = lags_dict,
                 steps              = 7,
                 transformer_series = StandardScaler(),
                 transformer_exog   = None,
                 weight_func        = None
             )

forecaster.fit(series=data_train)

# Predict
# ==============================================================================
predictions = forecaster.predict(steps=7)
display(predictions)

# Create and fit forecaster MultiVariate Custom lags with None # ============================================================================== lags_dict = { 'so2': [7, 14], 'co': None, 'no': [7, 14], 'no2': [7, 14], 'pm10': [7, 14], 'nox': [7, 14], 'o3': [7, 14], 'veloc.': 3, 'direc.': 3, 'pm2.5': [7, 14] } forecaster = ForecasterDirectMultiVariate( regressor = LGBMRegressor(random_state=123, verbose=-1), level = 'co', lags = lags_dict, steps = 7, transformer_series = StandardScaler(), transformer_exog = None, weight_func = None ) forecaster.fit(series=data_train) # Predict # ============================================================================== predictions = forecaster.predict(steps=7) display(predictions)

	co
2023-06-01	0.107966
2023-06-02	0.118692
2023-06-03	0.125480
2023-06-04	0.132908
2023-06-05	0.118237
2023-06-06	0.121638
2023-06-07	0.120753

It is possible to use the create_train_X_y method to generate the matrices that the forecaster is using to train the model. This approach enables gaining insight into the specific lags that have been created.

In [20]:

# Extract training matrix
# ==============================================================================
X_train, y_train = forecaster.create_train_X_y(series=data_train)

# X and y to train model for step 1
X_train_step_1, y_train_step_1 = forecaster.filter_train_X_y_for_step(
                                     step    = 1,
                                     X_train = X_train,
                                     y_train = y_train,
                                 )

X_train_step_1.head(4)

# Extract training matrix # ============================================================================== X_train, y_train = forecaster.create_train_X_y(series=data_train) # X and y to train model for step 1 X_train_step_1, y_train_step_1 = forecaster.filter_train_X_y_for_step( step = 1, X_train = X_train, y_train = y_train, ) X_train_step_1.head(4)

Out[20]:

	so2_lag_7	so2_lag_14	no_lag_7	no_lag_14	no2_lag_7	no2_lag_14	pm10_lag_7	pm10_lag_14	nox_lag_7	nox_lag_14	o3_lag_7	o3_lag_14	veloc._lag_1	veloc._lag_2	veloc._lag_3	direc._lag_1	direc._lag_2	direc._lag_3	pm2.5_lag_7	pm2.5_lag_14
datetime
2019-01-15	1.061795	2.362414	3.462136	2.232968	2.971237	2.098158	1.175259	0.229121	3.419881	2.298657	-1.871669	-1.800847	-0.726869	-0.979544	-0.792953	0.673274	1.019948	1.581166	2.104497	1.084751
2019-01-16	1.805006	2.408865	6.247303	3.270300	2.622404	3.254290	1.156585	0.599485	4.605306	3.486375	-1.754371	-2.256761	-1.150585	-0.726869	-0.979544	0.171311	0.673274	1.019948	1.782163	1.108193
2019-01-17	-0.982034	2.269513	0.826174	6.311248	2.596491	3.629037	-0.119456	1.327762	1.927209	5.208336	-0.331300	-2.356354	-0.944558	-1.150585	-0.726869	0.511174	0.171311	0.673274	-0.374541	1.705975
2019-01-18	1.479852	1.758556	8.194077	2.886629	4.617729	2.911437	1.221944	1.032094	6.726230	3.096583	-1.433461	-2.073068	-1.115600	-0.944558	-1.150585	1.436094	0.511174	0.171311	0.815163	1.782163

In [21]:

# Extract training matrix
# ==============================================================================
y_train_step_1.head(4)

# Extract training matrix # ============================================================================== y_train_step_1.head(4)

Out[21]:

datetime
2019-01-15    3.149604
2019-01-16    1.554001
2019-01-17   -0.323179
2019-01-18   -0.417038
Freq: D, Name: co_step_1, dtype: float64

Exogenous variables in MultiVariate¶

Exogenous variables are predictors that are independent of the model being used for forecasting, and their future values must be known in order to include them in the prediction process.

In the ForecasterDirectMultiVariate, as in the other forecasters, exogenous variables can be easily included as predictors using the exog argument.

To learn more about exogenous variables in skforecast visit the exogenous variables user guide.

Scikit-learn transformers in MultiVariate¶

By default, the ForecasterDirectMultiVariate class uses the scikit-learn StandardScaler transformer to scale the data. This transformer is applied to all series. However, it is possible to use different transformers for each series or not to apply any transformation at all:

• If transformer_series is a transformer the same transformation will be applied to all series.

• If transformer_series is a dict a different transformation can be set for each series. Series not present in the dict will not have any transformation applied to them (check warning message).

Learn more about using scikit-learn transformers with skforecast.

In [22]:

# Transformers in MultiVariate
# ==============================================================================
forecaster = ForecasterDirectMultiVariate(
                 regressor          = LGBMRegressor(random_state=123, verbose=-1),
                 level              = 'co',
                 lags               = 7,
                 steps              = 7,
                 transformer_series = {'co': StandardScaler(), 'no2': StandardScaler()},
                 transformer_exog   = None,
                 weight_func        = None,
             )

forecaster.fit(series=data_train)
forecaster

# Transformers in MultiVariate # ============================================================================== forecaster = ForecasterDirectMultiVariate( regressor = LGBMRegressor(random_state=123, verbose=-1), level = 'co', lags = 7, steps = 7, transformer_series = {'co': StandardScaler(), 'no2': StandardScaler()}, transformer_exog = None, weight_func = None, ) forecaster.fit(series=data_train) forecaster

c:\Users\jaesc2\Miniconda3\envs\skforecast_py11_2\Lib\site-packages\skforecast\utils\utils.py:363: IgnoredArgumentWarning: {'o3', 'direc.', 'nox', 'no', 'pm10', 'so2', 'pm2.5', 'veloc.'} not present in `transformer_series`. No transformation is applied to these series. 
 You can suppress this warning using: warnings.simplefilter('ignore', category=IgnoredArgumentWarning)
  warnings.warn(

Out[22]:

ForecasterDirectMultiVariate

General Information

• Regressor: LGBMRegressor
• Target series (level): co
• Lags: [1 2 3 4 5 6 7]
• Window features: None
• Window size: 7
• Maximum steps to predict: 7
• Exogenous included: False
• Weight function included: False
• Differentiation order: None
• Creation date: 2024-11-11 12:11:30
• Last fit date: 2024-11-11 12:11:32
• Skforecast version: 0.14.0
• Python version: 3.11.10
• Forecaster id: None

Exogenous Variables

None

Data Transformations

• Transformer for series: 'co': StandardScaler(), 'no2': StandardScaler()
• Transformer for exog: None

Training Information

• Target series (level): co
• Multivariate series: so2, co, no, no2, pm10, nox, o3, veloc., direc., pm2.5
• Training range: [Timestamp('2019-01-01 00:00:00'), Timestamp('2023-05-31 00:00:00')]
• Training index type: DatetimeIndex
• Training index frequency: D

Regressor Parameters

{'boosting_type': 'gbdt', 'class_weight': None, 'colsample_bytree': 1.0, 'importance_type': 'split', 'learning_rate': 0.1, 'max_depth': -1, 'min_child_samples': 20, 'min_child_weight': 0.001, 'min_split_gain': 0.0, 'n_estimators': 100, 'n_jobs': None, 'num_leaves': 31, 'objective': None, 'random_state': 123, 'reg_alpha': 0.0, 'reg_lambda': 0.0, 'subsample': 1.0, 'subsample_for_bin': 200000, 'subsample_freq': 0, 'verbose': -1}

Fit Kwargs

{}

🛈 API Reference    🗎 User Guide

Weights in MultiVariate¶

The weights are used to control the influence that each observation has on the training of the model.

Learn more about weighted time series forecasting with skforecast.

In [23]:

# Weights in MultiVariate
# ==============================================================================
def custom_weights(index):
    """
    Return 0 if index is between '2013-01-01' and '2013-01-31', 1 otherwise.
    """
    weights = np.where(
                  (index >= '2013-01-01') & (index <= '2013-01-31'),
                   0,
                   1
              )
    
    return weights


forecaster = ForecasterDirectMultiVariate(
                 regressor          = LGBMRegressor(random_state=123, verbose=-1),
                 level              = 'co',
                 lags               = 7,
                 steps              = 7,
                 transformer_series = StandardScaler(),
                 transformer_exog   = None,
                 weight_func        = custom_weights
             )

forecaster.fit(series=data_train)
forecaster.predict(steps=7).head(3)

# Weights in MultiVariate # ============================================================================== def custom_weights(index): """ Return 0 if index is between '2013-01-01' and '2013-01-31', 1 otherwise. """ weights = np.where( (index >= '2013-01-01') & (index <= '2013-01-31'), 0, 1 ) return weights forecaster = ForecasterDirectMultiVariate( regressor = LGBMRegressor(random_state=123, verbose=-1), level = 'co', lags = 7, steps = 7, transformer_series = StandardScaler(), transformer_exog = None, weight_func = custom_weights ) forecaster.fit(series=data_train) forecaster.predict(steps=7).head(3)

Out[23]:

	co
2023-06-01	0.106243
2023-06-02	0.103617
2023-06-03	0.102537

⚠ Warning

The weight_func argument will be ignored if the regressor does not accept sample_weight in its fit method.

The source code of the weight_func added to the forecaster is stored in the argument source_code_weight_func.

In [24]:

# Source code weight function
# ==============================================================================
print(forecaster.source_code_weight_func)

# Source code weight function # ============================================================================== print(forecaster.source_code_weight_func)

def custom_weights(index):
    """
    Return 0 if index is between '2013-01-01' and '2013-01-31', 1 otherwise.
    """
    weights = np.where(
                  (index >= '2013-01-01') & (index <= '2013-01-31'),
                   0,
                   1
              )
    
    return weights

Compare multiple metrics¶

All four functions (backtesting_forecaster_multiseries, grid_search_forecaster_multiseries, random_search_forecaster_multiseries, and bayesian_search_forecaster_multiseries) allow the calculation of multiple metrics for each forecaster configuration if a list is provided. This list can include custom metrics, and the best model is selected based on the first metric in the list and the first aggregation method (if more than one is provided).

In [25]:

# Grid search MultiVariate with multiple metrics
# ==============================================================================
forecaster = ForecasterDirectMultiVariate(
                 regressor          = LGBMRegressor(random_state=123, verbose=-1),
                 level              = 'co',
                 lags               = 7,
                 steps              = 7
             )    

def custom_metric(y_true, y_pred):
    """
    Calculate the mean absolute error using only the predicted values of the last
    3 months of the year.
    """
    mask = y_true.index.month.isin([10, 11, 12])
    metric = mean_absolute_error(y_true[mask], y_pred[mask])
    
    return metric

cv = TimeSeriesFold(
         steps              = 7,
         initial_train_size = len(data_train),
         refit              = False,
     )

lags_grid = [7, 14]
param_grid = {'alpha': [0.01, 0.1, 1]}

results = grid_search_forecaster_multiseries(
              forecaster       = forecaster,
              series           = data,
              exog             = None,
              lags_grid        = lags_grid,
              param_grid       = param_grid,
              cv               = cv,
              metric           = [mean_absolute_error, custom_metric, 'mean_squared_error'],
              aggregate_metric = 'weighted_average',
              return_best      = True,
              n_jobs           = 'auto',
              verbose          = False,
              show_progress    = True
          )

results

# Grid search MultiVariate with multiple metrics # ============================================================================== forecaster = ForecasterDirectMultiVariate( regressor = LGBMRegressor(random_state=123, verbose=-1), level = 'co', lags = 7, steps = 7 ) def custom_metric(y_true, y_pred): """ Calculate the mean absolute error using only the predicted values of the last 3 months of the year. """ mask = y_true.index.month.isin([10, 11, 12]) metric = mean_absolute_error(y_true[mask], y_pred[mask]) return metric cv = TimeSeriesFold( steps = 7, initial_train_size = len(data_train), refit = False, ) lags_grid = [7, 14] param_grid = {'alpha': [0.01, 0.1, 1]} results = grid_search_forecaster_multiseries( forecaster = forecaster, series = data, exog = None, lags_grid = lags_grid, param_grid = param_grid, cv = cv, metric = [mean_absolute_error, custom_metric, 'mean_squared_error'], aggregate_metric = 'weighted_average', return_best = True, n_jobs = 'auto', verbose = False, show_progress = True ) results

lags grid:   0%|          | 0/2 [00:00<?, ?it/s]

params grid:   0%|          | 0/3 [00:00<?, ?it/s]

`Forecaster` refitted using the best-found lags and parameters, and the whole data set: 
  Lags: [ 1  2  3  4  5  6  7  8  9 10 11 12 13 14] 
  Parameters: {'alpha': 0.01}
  Backtesting metric: 0.014486558378954958
  Levels: ['co']

Out[25]:

	levels	lags	lags_label	params	mean_absolute_error	custom_metric	mean_squared_error	alpha
0	[co]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	{'alpha': 0.01}	0.014487	0.021981	0.000439	0.01
1	[co]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	{'alpha': 0.1}	0.014487	0.021981	0.000439	0.10
2	[co]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]	{'alpha': 1}	0.014487	0.021981	0.000439	1.00
3	[co]	[1, 2, 3, 4, 5, 6, 7]	[1, 2, 3, 4, 5, 6, 7]	{'alpha': 0.01}	0.014773	0.022789	0.000511	0.01
4	[co]	[1, 2, 3, 4, 5, 6, 7]	[1, 2, 3, 4, 5, 6, 7]	{'alpha': 0.1}	0.014773	0.022789	0.000511	0.10
5	[co]	[1, 2, 3, 4, 5, 6, 7]	[1, 2, 3, 4, 5, 6, 7]	{'alpha': 1}	0.014773	0.022789	0.000511	1.00

Feature importances¶

Since ForecasterDirectMultiVariate fits one model per step, it is necessary to specify from which model retrieves its feature importances.

In [26]:

# Feature importances for step 1
# ==============================================================================
forecaster.get_feature_importances(step=1)

# Feature importances for step 1 # ============================================================================== forecaster.get_feature_importances(step=1)

Out[26]:

	feature	importance
14	co_lag_1	146
31	no_lag_4	84
61	pm10_lag_6	64
1	so2_lag_2	52
0	so2_lag_1	50
...	...	...
47	no2_lag_6	8
131	pm2.5_lag_6	8
132	pm2.5_lag_7	7
82	nox_lag_13	5
54	no2_lag_13	3

140 rows × 2 columns

Training and prediction matrices¶

While the primary goal of building forecasting models is to predict future values, it is equally important to evaluate if the model is effectively learning from the training data. Analyzing predictions on the training data or exploring the prediction matrices is crucial for assessing model performance and understanding areas for optimization. This process can help identify issues like overfitting or underfitting, as well as provide deeper insights into the model’s decision-making process. Check the How to Extract Training and Prediction Matrices user guide for more information.