Data drift detection¶
In the context of forecasting and machine learning, data drift refers to a change in the statistical properties of the input data over time compared to the data on which the model was originally trained. When this happens, the model may start to produce less accurate or unreliable predictions, since it no longer generalizes well to the new data distribution.
Data drift can take several forms:
Covariate Drift (Feature Drift): The distribution of the input features changes, but the relationship between features and target remains the same. Example: A model was trained when a feature had values in a certain range. Over time, if that feature shifts to a different range, covariate drift occurs.
Prior Probability Drift (Label Drift): The distribution of the target variable changes. Example: A model trained to predict energy consumption during a season may fail if seasonal patterns change due to external factors.
Concept Drift: The relationship between input features and the target variable changes. Example: A model predicting energy consumption from weather data might fail if new technologies or behaviors alter how weather affects energy usage.
Detecting and addressing data drift is crucial for maintaining model reliability in production environments. Common strategies include:
Monitoring input data during prediction to detect changes early.
Tracking model performance metrics (e.g., accuracy, precision, recall) over time.
Retraining models periodically with recent data to adapt to evolving conditions.
Skforecast includes two dedicated classes for data drift detection:
PopulationDriftDetector: detects changes at the population level, helping identify when a forecasting model should be retrained.RangeDriftDetector: detects changes at the single-observation level, suitable for validating input data during the prediction phase.
Drift detection during model training¶
The PopulationDriftDetector is designed to detect feature drift and label drift in time series data. It evaluates whether the distribution of the input variables (both target and exogenous) remains consistent with the data used to train the forecasting model.
By comparing recent observations with the training data, the detector identifies significant distributional changes that may indicate the model needs retraining.
The statistical metrics used depend on the data type:
Numerical features: Kolmogorov–Smirnov statistic and Jensen–Shannon distance.
Categorical features: Chi-squared statistic and Jensen–Shannon distance.
The API follows the same design principles as Skforecast forecasters:
The same data used to train a forecaster can also be used to fit a
PopulationDriftDetector.When new historical data becomes available (i.e., multiple new observations), the
predictmethod can be used to check for drift.If drift is detected, users should analyze its cause and consider retraining or recalibrating the forecasting model.
✎ Note
This implementation is inspired by NannyML's DriftDetector, but provides a lightweight adaptation tailored to Skforecast’s time series context.
- Memory-efficient: The detector does not store the full reference data. Instead, it keeps only the precomputed statistics required to evaluate drift efficiently during prediction.
- Empirical thresholds: All thresholds are derived from the specified quantile of the empirical distributions computed from the reference data chunks.
- Out-of-range detection: It also checks for out-of-range values in numerical features and for unseen categories in categorical features.
- Multiple time series support: It can handle multiple time series, each one with its own exogenous variables.
For an in-depth explanation of the underlying calculations, see Deep dive into temporal drift detection in time series.
If user requires more advanced features, such as multivariate drift detection or data quality checks, consider using NannyML directly.
To illustrate how drift detection works, the dataset is divided into a training set and a new data partition, simulating a real-world scenario where additional data becomes available after the model has been trained.
To emulate data drift, the variable temp in the new data partition is intentionally modified:
June: Temperatures are increased by +10 ºC.
July: Temperatures are increased by +20 ºC.
October: Temperatures are replaced by a constant value equal to the mean of the original data. Although this value lies within the original range, its lack of variability makes it statistically atypical.
December: Temperatures are decreased by -10 ºC.
The variable hum remains unchanged throughout the new data partition, serving as a control variable to demonstrate that the drift detector correctly identifies no drift when none exists.
# Libraries
# ==============================================================================
import pandas as pd
import matplotlib.pyplot as plt
from skforecast.datasets import fetch_dataset
from skforecast.plot import set_dark_theme
from skforecast.drift_detection import PopulationDriftDetector
# Data
# ==============================================================================
data = fetch_dataset('bike_sharing', verbose=False)
data = data[['temp', 'hum']]
display(data.head())
data_train = data.iloc[: 9000].copy()
data_new = data.iloc[9000:].copy()
| temp | hum | |
|---|---|---|
| date_time | ||
| 2011-01-01 00:00:00 | 9.84 | 81.0 |
| 2011-01-01 01:00:00 | 9.02 | 80.0 |
| 2011-01-01 02:00:00 | 9.02 | 80.0 |
| 2011-01-01 03:00:00 | 9.84 | 75.0 |
| 2011-01-01 04:00:00 | 9.84 | 75.0 |
# Inject changes in the distribution
# ==============================================================================
data_new_drift = data_new.copy()
# Sum +10 to observations of june 2012
data_new_drift.loc['2012-06-01 00:00:00':'2012-06-30 23:00:00', 'temp'] = (
data_new_drift.loc['2012-06-01 00:00:00':'2012-06-30 23:00:00', 'temp'] + 10
)
# Sum +20 to observations of july 2012
data_new_drift.loc['2012-07-01 00:00:00':'2012-07-31 23:00:00', 'temp'] = (
data_new_drift.loc['2012-07-01 00:00:00':'2012-07-31 23:00:00', 'temp'] + 20
)
# Constant mean value in October 2012
data_new_drift.loc['2012-10-01 00:00:00':'2012-10-31 23:00:00', 'temp'] = (
data_new_drift.loc['2012-10-01 00:00:00':'2012-10-31 23:00:00', 'temp'].mean()
)
# Substract -10 to december 2012
data_new_drift.loc['2012-12-01 00:00:00':'2012-12-31 23:00:00', 'temp'] = (
data_new_drift.loc['2012-12-01 00:00:00':'2012-12-31 23:00:00', 'temp'] - 10
)
# Plot
# ==============================================================================
set_dark_theme()
fig, ax = plt.subplots(figsize=(8, 4))
data_train.loc[:, 'temp'].plot(ax=ax, label='Train')
data_new_drift.loc[:, 'temp'].plot(ax=ax, label='Test with drift', color='red')
data_new.loc[:, 'temp'].plot(ax=ax, label='Test', color='green')
ax.axhline(data_train['temp'].max(), color='white', linestyle=':', label='Max Train')
ax.axhline(data_train['temp'].min(), color='white', linestyle=':', label='Min Train')
ax.set_xlabel("")
ax.legend()
plt.show();
When creating a PopulationDriftDetector instance, two key arguments must be specified:
chunk_size: Defines the number of observations in each data chunk used to compare distributions. A smaller chunk size enables more frequent drift checks but can increase false positives due to higher variability. Conversely, a larger chunk size smooths out variability but may delay drift detection. The optimal value depends on the trade-off between sensitivity and stability for the specific application and dataset.threshold: Specifies the percentile threshold used to determine whether drift has occurred. The higher the threshold, the more conservative the detector will be in flagging drift.
# Fit detector using the training data
# ==============================================================================
detector = PopulationDriftDetector(
chunk_size = 'ME', # Monthly chunks
threshold = 0.95
)
detector.fit(data_train)
detector
PopulationDriftDetector
General Information
- Fitted features: ['temp', 'hum']
- Is fitted: True
Once the detector has been fitted, it can be used to evaluate new data using the predict method. This method returns two DataFrames:
Detailed results: Contain information about the computed statistics, thresholds, and drift status for each data chunk.
Summary results: Provide an overview showing the number and percentage of chunks where drift was detected.
# Detect drift in new data
# ==============================================================================
drift_results, drift_summary = detector.predict(data_new_drift)
# Drift detailed results
# ==============================================================================
drift_results
| chunk | chunk_start | chunk_end | feature | ks_statistic | threshold_ks | chi2_statistic | threshold_chi2 | jensen_shannon | threshold_js | reference_range | is_out_of_range | drift_ks_statistic | drift_chi2_statistic | drift_js | drift_detected | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2012-01-11 | 2012-01-31 23:00:00 | temp | 0.490175 | 0.682966 | NaN | NaN | 0.546958 | 0.689223 | (0.8200000000000001, 39.36) | False | False | False | False | False |
| 1 | 1 | 2012-02-01 | 2012-02-29 23:00:00 | temp | 0.477663 | 0.682966 | NaN | NaN | 0.523748 | 0.689223 | (0.8200000000000001, 39.36) | False | False | False | False | False |
| 2 | 2 | 2012-03-01 | 2012-03-31 23:00:00 | temp | 0.232412 | 0.682966 | NaN | NaN | 0.373938 | 0.689223 | (0.8200000000000001, 39.36) | False | False | False | False | False |
| 3 | 3 | 2012-04-01 | 2012-04-30 23:00:00 | temp | 0.217000 | 0.682966 | NaN | NaN | 0.455947 | 0.689223 | (0.8200000000000001, 39.36) | False | False | False | False | False |
| 4 | 4 | 2012-05-01 | 2012-05-31 23:00:00 | temp | 0.443082 | 0.682966 | NaN | NaN | 0.539446 | 0.689223 | (0.8200000000000001, 39.36) | False | False | False | False | False |
| 5 | 5 | 2012-06-01 | 2012-06-30 23:00:00 | temp | 0.902111 | 0.682966 | NaN | NaN | 0.877304 | 0.689223 | (0.8200000000000001, 39.36) | True | True | False | True | True |
| 6 | 6 | 2012-07-01 | 2012-07-31 23:00:00 | temp | 1.000000 | 0.682966 | NaN | NaN | 1.000000 | 0.689223 | (0.8200000000000001, 39.36) | True | True | False | True | True |
| 7 | 7 | 2012-08-01 | 2012-08-31 23:00:00 | temp | 0.637269 | 0.682966 | NaN | NaN | 0.652528 | 0.689223 | (0.8200000000000001, 39.36) | False | False | False | False | False |
| 8 | 8 | 2012-09-01 | 2012-09-30 23:00:00 | temp | 0.446389 | 0.682966 | NaN | NaN | 0.518331 | 0.689223 | (0.8200000000000001, 39.36) | False | False | False | False | False |
| 9 | 9 | 2012-10-01 | 2012-10-31 23:00:00 | temp | 0.537556 | 0.682966 | NaN | NaN | 0.863793 | 0.689223 | (0.8200000000000001, 39.36) | False | False | False | True | True |
| 10 | 10 | 2012-11-01 | 2012-11-30 23:00:00 | temp | 0.468611 | 0.682966 | NaN | NaN | 0.562611 | 0.689223 | (0.8200000000000001, 39.36) | False | False | False | False | False |
| 11 | 11 | 2012-12-01 | 2012-12-31 23:00:00 | temp | 0.860731 | 0.682966 | NaN | NaN | 0.843966 | 0.689223 | (0.8200000000000001, 39.36) | True | True | False | True | True |
| 12 | 0 | 2012-01-11 | 2012-01-31 23:00:00 | hum | 0.130825 | 0.310789 | NaN | NaN | 0.152290 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 13 | 1 | 2012-02-01 | 2012-02-29 23:00:00 | hum | 0.161425 | 0.310789 | NaN | NaN | 0.199334 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 14 | 2 | 2012-03-01 | 2012-03-31 23:00:00 | hum | 0.119387 | 0.310789 | NaN | NaN | 0.150733 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 15 | 3 | 2012-04-01 | 2012-04-30 23:00:00 | hum | 0.278944 | 0.310789 | NaN | NaN | 0.328472 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 16 | 4 | 2012-05-01 | 2012-05-31 23:00:00 | hum | 0.093703 | 0.310789 | NaN | NaN | 0.205141 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 17 | 5 | 2012-06-01 | 2012-06-30 23:00:00 | hum | 0.171722 | 0.310789 | NaN | NaN | 0.240059 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 18 | 6 | 2012-07-01 | 2012-07-31 23:00:00 | hum | 0.103219 | 0.310789 | NaN | NaN | 0.178075 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 19 | 7 | 2012-08-01 | 2012-08-31 23:00:00 | hum | 0.110520 | 0.310789 | NaN | NaN | 0.196713 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 20 | 8 | 2012-09-01 | 2012-09-30 23:00:00 | hum | 0.076111 | 0.310789 | NaN | NaN | 0.196889 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 21 | 9 | 2012-10-01 | 2012-10-31 23:00:00 | hum | 0.125477 | 0.310789 | NaN | NaN | 0.217908 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 22 | 10 | 2012-11-01 | 2012-11-30 23:00:00 | hum | 0.217556 | 0.310789 | NaN | NaN | 0.280111 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
| 23 | 11 | 2012-12-01 | 2012-12-31 23:00:00 | hum | 0.096502 | 0.310789 | NaN | NaN | 0.187856 | 0.345842 | (0.0, 100.0) | False | False | False | False | False |
# Drift summary
# ==============================================================================
drift_summary
| feature | n_chunks_with_drift | pct_chunks_with_drift | |
|---|---|---|---|
| 0 | hum | 0 | 0.000000 |
| 1 | temp | 4 | 33.333333 |
As expected, the detector identifies drift in the modified new data, while no drift is detected in unaltered data.
# Higlhlight chunks with detected drift
# ==============================================================================
set_dark_theme()
fig, ax = plt.subplots(figsize=(8, 4))
data_train.loc[:, 'temp'].plot(ax=ax, label='Train')
data_new_drift.loc[:, 'temp'].plot(ax=ax, label='New data with drift', color='red')
data_new.loc[:, 'temp'].plot(ax=ax, label='New data', color='green')
ax.axhline(data_train['temp'].max(), color='white', linestyle=':', label='Max Train')
ax.axhline(data_train['temp'].min(), color='white', linestyle=':', label='Min Train')
for row in drift_results.query('drift_detected == True').itertuples():
chunk_start = row.chunk_start
chunk_end = row.chunk_end
drift_detected = row.drift_detected
if drift_detected:
ax.axvspan(chunk_start, chunk_end, color='red', alpha=0.3, label='Drift detected')
# Remove repetitive labels in legend
handles, labels = ax.get_legend_handles_labels()
by_label = dict(zip(labels, handles))
ax.legend(by_label.values(), by_label.keys())
ax.set_xlabel("")
plt.show();
PopulationDriftDetector can be used with multiple time series simultaneously, each one with its own features. In this case, the input data must be a pandas DataFrame with a MultiIndex, where the first level is the series identifier, and the second level corresponds to the temporal index.
# Multi-series data
# ==============================================================================
data_multiseries = pd.concat(
[
data.assign(series='series_1'),
data.assign(series='series_2'),
data.assign(series='series_3')
]
).set_index('series', append=True).swaplevel(0,1)
display(data_multiseries)
# Split train/test per series
data_multiseries_train = (
data_multiseries
.groupby(level='series', group_keys=False)
.apply(lambda x: x.iloc[:9000])
)
data_multiseries_new = (
data_multiseries
.groupby(level='series', group_keys=False)
.apply(lambda x: x.iloc[9000:])
)
| temp | hum | ||
|---|---|---|---|
| series | date_time | ||
| series_1 | 2011-01-01 00:00:00 | 9.84 | 81.0 |
| 2011-01-01 01:00:00 | 9.02 | 80.0 | |
| 2011-01-01 02:00:00 | 9.02 | 80.0 | |
| 2011-01-01 03:00:00 | 9.84 | 75.0 | |
| 2011-01-01 04:00:00 | 9.84 | 75.0 | |
| ... | ... | ... | ... |
| series_3 | 2012-12-31 19:00:00 | 10.66 | 60.0 |
| 2012-12-31 20:00:00 | 10.66 | 60.0 | |
| 2012-12-31 21:00:00 | 10.66 | 60.0 | |
| 2012-12-31 22:00:00 | 10.66 | 56.0 | |
| 2012-12-31 23:00:00 | 10.66 | 65.0 |
52632 rows × 2 columns
detector = PopulationDriftDetector(
chunk_size='ME',
threshold=0.95
)
detector.fit(data_multiseries_train)
detector
PopulationDriftDetector
General Information
- Fitted features: {'series_1': ['temp', 'hum'], 'series_2': ['temp', 'hum'], 'series_3': ['temp', 'hum']}
- Is fitted: True
drift_results, drift_summary = detector.predict(data_multiseries_new)
drift_summary
| series_id | feature | n_chunks_with_drift | pct_chunks_with_drift | |
|---|---|---|---|---|
| 0 | series_1 | hum | 0 | 0.000000 |
| 1 | series_1 | temp | 2 | 16.666667 |
| 2 | series_2 | hum | 0 | 0.000000 |
| 3 | series_2 | temp | 2 | 16.666667 |
| 4 | series_3 | hum | 0 | 0.000000 |
| 5 | series_3 | temp | 2 | 16.666667 |
Drift detection during prediction¶
Skforecast provides the class RangeDriftDetector to detect covariate drift in both single and multiple time series, as well as in exogenous variables.
The detector checks whether the input data (lags and exogenous variables) used to predict new values fall within the range of the data used to train the model.
Its API follows the same design as the forecasters:
The data used to train a forecaster can also be used to fit the
RangeDriftDetector.The data passed to the forecaster's
predictmethod can be also passed to theRangeDriftDetector'spredictmethod to check for drift in the input data before making predictions.If drift is detected, users should analyze its cause and consider whether the model is still appropriate for making predictions with the new data.
# Libraries
# ==============================================================================
import numpy as np
import pandas as pd
from sklearn.ensemble import HistGradientBoostingRegressor
from skforecast.datasets import fetch_dataset
from skforecast.recursive import ForecasterRecursive
from skforecast.drift_detection import RangeDriftDetector
Detecting out-of-range values in a single series¶
The RangeDriftDetector checks whether the values of a time series remain consistent with the data seen during training.
For numeric variables, it verifies that each new value falls within the minimum and maximum range of the training data. Values outside this range are flagged as potential drift.
For categorical variables, it checks whether each new category was observed during training. Unseen categories are flagged as potential drift.
This mechanism allows you to quickly identify when the model is receiving inputs that differ from those it was trained on, helping you decide whether to retrain the model or adjust preprocessing.
# Simulated data
# ==============================================================================
rgn = np.random.default_rng(123)
y_train = pd.Series(
rgn.normal(loc=10, scale=2, size=100),
index=pd.date_range(start="2020-01-01", periods=100),
name="y",
)
exog_train = pd.DataFrame(
{
"exog_1": rgn.normal(loc=10, scale=2, size=100),
"exog_2": rgn.choice(["A", "B", "C", "D", "E"], size=100),
},
index=y_train.index,
)
display(y_train.head())
display(exog_train.head())
2020-01-01 8.021757 2020-01-02 9.264427 2020-01-03 12.575851 2020-01-04 10.387949 2020-01-05 11.840462 Freq: D, Name: y, dtype: float64
| exog_1 | exog_2 | |
|---|---|---|
| 2020-01-01 | 8.968465 | B |
| 2020-01-02 | 13.316227 | B |
| 2020-01-03 | 9.405475 | A |
| 2020-01-04 | 7.233246 | A |
| 2020-01-05 | 9.437591 | A |
# Train RangeDriftDetector
# ==============================================================================
detector = RangeDriftDetector()
detector.fit(y=y_train, exog=exog_train)
detector
RangeDriftDetector
General Information
- Fitted series: y
- Fitted exogenous: exog_1, exog_2
- Series-specific exogenous: False
- Is fitted: True
Series value ranges
-
{'y': (5.5850578036003915, 14.579819894629157)}
Exogenous value ranges
-
{'exog_1': (4.5430286262543085, 14.531041199734418), 'exog_2': {'B', 'D', 'C', 'E', 'A'}}
Lets assume the model is deployed in production and new data is being used to forecast future values. We simulate a covariate drift in the target series and in the exogenous variables to illustrate how to use the RangeDriftDetector class to detect it.
# Prediction with drifted data
# ==============================================================================
last_window = pd.Series(
[6.6, 7.5, 100, 9.3, 10.2], name="y"
) # Value 100 is out of range
exog_predict = pd.DataFrame(
{
"exog_1": [8, 9, 10, 70, 12], # Value 70 is out of range
"exog_2": ["A", "B", "C", "D", "W"], # Value 'W' is out of range
}
)
flag_out_of_range, series_out_of_range, exog_out_of_range = detector.predict(
last_window = last_window,
exog = exog_predict,
verbose = True,
suppress_warnings = False
)
print("Out of range detected :", flag_out_of_range)
print("Series out of range :", series_out_of_range)
print("Exogenous out of range :", exog_out_of_range)
╭────────────────────────────── FeatureOutOfRangeWarning ──────────────────────────────╮ │ 'y' has values outside the range seen during training [5.58506, 14.57982]. This may │ │ affect the accuracy of the predictions. │ │ │ │ Category : skforecast.exceptions.FeatureOutOfRangeWarning │ │ Location : │ │ c:\Users\jaesc2\Miniconda3\envs\skforecast_py12\Lib\site-packages\skforecast\drift_d │ │ etection\_range_drift.py:283 │ │ Suppress : warnings.simplefilter('ignore', category=FeatureOutOfRangeWarning) │ ╰──────────────────────────────────────────────────────────────────────────────────────╯
╭────────────────────────────── FeatureOutOfRangeWarning ──────────────────────────────╮ │ 'exog_1' has values outside the range seen during training [4.54303, 14.53104]. This │ │ may affect the accuracy of the predictions. │ │ │ │ Category : skforecast.exceptions.FeatureOutOfRangeWarning │ │ Location : │ │ c:\Users\jaesc2\Miniconda3\envs\skforecast_py12\Lib\site-packages\skforecast\drift_d │ │ etection\_range_drift.py:283 │ │ Suppress : warnings.simplefilter('ignore', category=FeatureOutOfRangeWarning) │ ╰──────────────────────────────────────────────────────────────────────────────────────╯
╭────────────────────────────── FeatureOutOfRangeWarning ──────────────────────────────╮ │ 'exog_2' has values not seen during training. Seen values: {'B', 'D', 'C', 'E', │ │ 'A'}. This may affect the accuracy of the predictions. │ │ │ │ Category : skforecast.exceptions.FeatureOutOfRangeWarning │ │ Location : │ │ c:\Users\jaesc2\Miniconda3\envs\skforecast_py12\Lib\site-packages\skforecast\drift_d │ │ etection\_range_drift.py:283 │ │ Suppress : warnings.simplefilter('ignore', category=FeatureOutOfRangeWarning) │ ╰──────────────────────────────────────────────────────────────────────────────────────╯
╭───────────────────────────── Out-of-range summary ──────────────────────────────╮ │ Series: │ │ 'y' has values outside the observed range [5.58506, 14.57982]. │ │ │ │ Exogenous Variables: │ │ 'exog_1' has values outside the observed range [4.54303, 14.53104]. │ │ 'exog_2' has values not seen during training. Seen values: {'B', 'D', 'C', 'E', │ │ 'A'}. │ ╰─────────────────────────────────────────────────────────────────────────────────╯
Out of range detected : True Series out of range : ['y'] Exogenous out of range : ['exog_1', 'exog_2']
Detecting out-of-range values in multiple series¶
The same process applies when modeling multiple time series.
For each series, the
RangeDriftDetectorchecks whether the new values remain within the range of the training data.If exogenous variables are included, they are checked grouped by series, ensuring that drift is detected in the correct context.
This allows you to monitor drift at the per-series level, making it easier to spot issues in specific series without being misled by aggregated results.
# Simulated data - Multiple time series
# ==============================================================================
idx = pd.MultiIndex.from_product(
[
["series_1", "series_2", "series_3"],
pd.date_range(start="2020-01-01", periods=3),
],
names=["series_id", "datetime"],
)
series_train = pd.DataFrame(
{"values": [1, 2, 3, 10, 20, 30, 100, 200, 300]}, index=idx
)
exog_train = pd.DataFrame(
{
"exog_1": [5.0, 6.0, 7.0, 15.0, 25.0, 35.0, 150.0, 250.0, 350.0],
"exog_2": ["A", "B", "C", "D", "E", "F", "G", "H", "I"],
},
index=idx,
)
display(series_train)
display(exog_train)
| values | ||
|---|---|---|
| series_id | datetime | |
| series_1 | 2020-01-01 | 1 |
| 2020-01-02 | 2 | |
| 2020-01-03 | 3 | |
| series_2 | 2020-01-01 | 10 |
| 2020-01-02 | 20 | |
| 2020-01-03 | 30 | |
| series_3 | 2020-01-01 | 100 |
| 2020-01-02 | 200 | |
| 2020-01-03 | 300 |
| exog_1 | exog_2 | ||
|---|---|---|---|
| series_id | datetime | ||
| series_1 | 2020-01-01 | 5.0 | A |
| 2020-01-02 | 6.0 | B | |
| 2020-01-03 | 7.0 | C | |
| series_2 | 2020-01-01 | 15.0 | D |
| 2020-01-02 | 25.0 | E | |
| 2020-01-03 | 35.0 | F | |
| series_3 | 2020-01-01 | 150.0 | G |
| 2020-01-02 | 250.0 | H | |
| 2020-01-03 | 350.0 | I |
# Train RangeDriftDetector - Multiple time series
# ==============================================================================
detector = RangeDriftDetector()
detector.fit(series=series_train, exog=exog_train)
detector
RangeDriftDetector
General Information
- Fitted series: series_1, series_2, series_3
- Fitted exogenous: exog_1, exog_2
- Series-specific exogenous: True
- Is fitted: True
Series value ranges
-
{'series_1': (1.0, 3.0), 'series_2': (10.0, 30.0), 'series_3': (100.0, 300.0)}
Exogenous value ranges
-
{'series_1': {'exog_1': (5.0, 7.0), 'exog_2': {'B', 'A', 'C'}}, 'series_2': {'exog_1': (15.0, 35.0), 'exog_2': {'E', 'D', 'F'}}, 'series_3': {'exog_1': (150.0, 350.0), 'exog_2': {'I', 'G', 'H'}}}
# Prediction with drifted data - Multiple time series
# ==============================================================================
last_window = pd.DataFrame(
{
"series_1": np.array([1.5, 2.3]),
"series_2": np.array([100, 20]), # Value 100 is out of range
"series_3": np.array([110, 200]),
},
index=pd.date_range(start="2020-01-02", periods=2),
)
idx = pd.MultiIndex.from_product(
[
["series_1", "series_2", "series_3"],
pd.date_range(start="2020-01-04", periods=2),
],
names=["series_id", "datetime"],
)
exog_predict = pd.DataFrame(
{
"exog_1": [5.0, 6.1, 10, 70, 220, 290],
"exog_2": ["A", "B", "D", "F", "W", "E"],
},
index=idx,
)
display(last_window)
display(exog_predict)
| series_1 | series_2 | series_3 | |
|---|---|---|---|
| 2020-01-02 | 1.5 | 100 | 110 |
| 2020-01-03 | 2.3 | 20 | 200 |
| exog_1 | exog_2 | ||
|---|---|---|---|
| series_id | datetime | ||
| series_1 | 2020-01-04 | 5.0 | A |
| 2020-01-05 | 6.1 | B | |
| series_2 | 2020-01-04 | 10.0 | D |
| 2020-01-05 | 70.0 | F | |
| series_3 | 2020-01-04 | 220.0 | W |
| 2020-01-05 | 290.0 | E |
# Prediction with drifted data - Multiple time series
# ==============================================================================
flag_out_of_range, series_out_of_range, exog_out_of_range = detector.predict(
last_window = last_window,
exog = exog_predict,
verbose = True,
suppress_warnings = False
)
print("Out of range detected :", flag_out_of_range)
print("Series out of range :", series_out_of_range)
print("Exogenous out of range :", exog_out_of_range)
╭────────────────────────────── FeatureOutOfRangeWarning ──────────────────────────────╮ │ 'series_2' has values outside the range seen during training [10.00000, 30.00000]. │ │ This may affect the accuracy of the predictions. │ │ │ │ Category : skforecast.exceptions.FeatureOutOfRangeWarning │ │ Location : │ │ c:\Users\jaesc2\Miniconda3\envs\skforecast_py12\Lib\site-packages\skforecast\drift_d │ │ etection\_range_drift.py:283 │ │ Suppress : warnings.simplefilter('ignore', category=FeatureOutOfRangeWarning) │ ╰──────────────────────────────────────────────────────────────────────────────────────╯
╭────────────────────────────── FeatureOutOfRangeWarning ──────────────────────────────╮ │ 'series_2': 'exog_1' has values outside the range seen during training [15.00000, │ │ 35.00000]. This may affect the accuracy of the predictions. │ │ │ │ Category : skforecast.exceptions.FeatureOutOfRangeWarning │ │ Location : │ │ c:\Users\jaesc2\Miniconda3\envs\skforecast_py12\Lib\site-packages\skforecast\drift_d │ │ etection\_range_drift.py:283 │ │ Suppress : warnings.simplefilter('ignore', category=FeatureOutOfRangeWarning) │ ╰──────────────────────────────────────────────────────────────────────────────────────╯
╭────────────────────────────── FeatureOutOfRangeWarning ──────────────────────────────╮ │ 'series_3': 'exog_2' has values not seen during training. Seen values: {'I', 'G', │ │ 'H'}. This may affect the accuracy of the predictions. │ │ │ │ Category : skforecast.exceptions.FeatureOutOfRangeWarning │ │ Location : │ │ c:\Users\jaesc2\Miniconda3\envs\skforecast_py12\Lib\site-packages\skforecast\drift_d │ │ etection\_range_drift.py:283 │ │ Suppress : warnings.simplefilter('ignore', category=FeatureOutOfRangeWarning) │ ╰──────────────────────────────────────────────────────────────────────────────────────╯
╭────────────────────────────── Out-of-range summary ──────────────────────────────╮ │ Series: │ │ 'series_2' has values outside the observed range [10.00000, 30.00000]. │ │ │ │ Exogenous Variables: │ │ 'series_2': 'exog_1' has values outside the observed range [15.00000, 35.00000]. │ │ 'series_3': 'exog_2' has values not seen during training. Seen values: {'I', │ │ 'G', 'H'}. │ ╰──────────────────────────────────────────────────────────────────────────────────╯
Out of range detected : True
Series out of range : ['series_2']
Exogenous out of range : {'series_2': ['exog_1'], 'series_3': ['exog_2']}
Combining RangeDriftDetector with Forecasters¶
When deploying a forecaster in production, it is good practice to pair it with a drift detector. This ensures that both are trained on the same dataset, allowing the drift detector to verify the input data before the forecaster makes predictions.
# Data
# ==============================================================================
data = fetch_dataset(name='h2o_exog')
data.index.name = 'datetime'
data.head(3)
╭─────────────────────────────────── h2o_exog ────────────────────────────────────╮ │ Description: │ │ Monthly expenditure ($AUD) on corticosteroid drugs that the Australian health │ │ system had between 1991 and 2008. Two additional variables (exog_1, exog_2) are │ │ simulated. │ │ │ │ Source: │ │ Hyndman R (2023). fpp3: Data for Forecasting: Principles and Practice (3rd │ │ Edition). http://pkg.robjhyndman.com/fpp3package/, │ │ https://github.com/robjhyndman/fpp3package, http://OTexts.com/fpp3. │ │ │ │ URL: │ │ https://raw.githubusercontent.com/skforecast/skforecast- │ │ datasets/main/data/h2o_exog.csv │ │ │ │ Shape: 195 rows x 3 columns │ ╰─────────────────────────────────────────────────────────────────────────────────╯
| y | exog_1 | exog_2 | |
|---|---|---|---|
| datetime | |||
| 1992-04-01 | 0.379808 | 0.958792 | 1.166029 |
| 1992-05-01 | 0.361801 | 0.951993 | 1.117859 |
| 1992-06-01 | 0.410534 | 0.952955 | 1.067942 |
# Train Forecaster and RangeDriftDetector
# ==============================================================================
steps = 36
data_train = data.iloc[:-steps, :]
data_test = data.iloc[-steps:, :]
forecaster = ForecasterRecursive(
estimator = HistGradientBoostingRegressor(random_state=123),
lags = 15
)
detector = RangeDriftDetector()
forecaster.fit(
y = data_train['y'],
exog = data_train[['exog_1', 'exog_2']]
)
detector.fit(
series = data_train['y'],
exog = data_train[['exog_1', 'exog_2']]
)
If you use the last_window stored in the Forecaster, drift detection is unnecessary because it corresponds to the final window of the training data. In production environments, however, you may supply an external last_window from a different time period. In that case, drift detection is recommended.
In the example below, the external last_window is identical to the final training window, so no drift will be detected.
# Last window (same as forecaster.last_window_)
# ==============================================================================
last_window = data_train['y'].iloc[-forecaster.max_lag:]
last_window
datetime 2004-04-01 0.739986 2004-05-01 0.795129 2004-06-01 0.856803 2004-07-01 1.001593 2004-08-01 0.994864 2004-09-01 1.134432 2004-10-01 1.181011 2004-11-01 1.216037 2004-12-01 1.257238 2005-01-01 1.170690 2005-02-01 0.597639 2005-03-01 0.652590 2005-04-01 0.670505 2005-05-01 0.695248 2005-06-01 0.842263 Freq: MS, Name: y, dtype: float64
# Check data with RangeDriftDetector and predict with Forecaster
# ==============================================================================
detector.predict(
last_window = last_window,
exog = data_test[['exog_1', 'exog_2']],
verbose = True,
suppress_warnings = False
)
predictions = forecaster.predict(
steps = 36,
last_window = last_window,
exog = data_test[['exog_1', 'exog_2']]
)
╭───────────────── Out-of-range summary ─────────────────╮ │ Series: │ │ No series with out-of-range values found. │ │ │ │ Exogenous Variables: │ │ No exogenous variables with out-of-range values found. │ ╰────────────────────────────────────────────────────────╯
Deep dive into temporal drift detection in time series¶
The ultimate goal of drift detection is to answer a simple but important question: Is the distribution of new data different from the distribution of the training data?
The goal of drift detection is to answer a simple but crucial question: Is the distribution of new data different from that of the training data?
When there is no time component and the data points are independently and identically distributed (i.i.d.), this question is usually addressed using statistical tests. These tests measure some form of distance between the distributions of the two datasets and calculate a probability value (p-value) to determine whether the difference is large enough to suggest a significant change.
However, this approach cannot be directly applied to time series data, where distributions evolve naturally over time due to factors such as seasonality or trends. Detecting drift in this context therefore requires methods that explicitly account for these expected temporal dynamics.
To illustrate this concept, the following example compares two months of a time series against the full dataset. In this case, the tested months behave as expected, so no drift should be detected.
# Libraries
# ==============================================================================
import seaborn as sns
from scipy.stats import ks_2samp
# Data
# ==============================================================================
data = fetch_dataset('bike_sharing', verbose=False)
data = data[['temp', 'hum']]
display(data.head())
data_train = data.iloc[: 9000].copy()
data_new = data.iloc[9000:].copy()
| temp | hum | |
|---|---|---|
| date_time | ||
| 2011-01-01 00:00:00 | 9.84 | 81.0 |
| 2011-01-01 01:00:00 | 9.02 | 80.0 |
| 2011-01-01 02:00:00 | 9.02 | 80.0 |
| 2011-01-01 03:00:00 | 9.84 | 75.0 |
| 2011-01-01 04:00:00 | 9.84 | 75.0 |
fig, ax = plt.subplots(figsize=(7, 3))
test_data_starts = '2011-12-01 22:00:00'
test_data_ends = '2012-01-31 23:00:00'
reference_data = data_train.loc[:, 'temp'].copy()
test_data = data_train.loc[test_data_starts:test_data_ends, 'temp'].copy()
reference_data.plot(ax=ax, label='Reference data')
test_data.plot(ax=ax, label='New data')
ax.set_xlabel("")
ax.legend()
plt.show();
A Kolmogorov–Smirnov (KS) test is used to compare the distributions of the training data and the new data. The null hypothesis states that both samples are drawn from the same underlying distribution. If the resulting p-value falls below a chosen significance level (commonly 0.05), the null hypothesis is rejected, indicating that the distributions differ significantly — a potential sign of data drift.
# Kolmogorov-Smirnov test to compare both data sets
# ==============================================================================
ks_2samp(
reference_data,
test_data,
)
KstestResult(statistic=np.float64(0.4571829521829522), pvalue=np.float64(8.54562775188432e-166), statistic_location=np.float64(18.86), statistic_sign=np.int8(-1))
# Plots to compare both data sets
# ==============================================================================
fig, axs = plt.subplots(ncols=2, figsize=(9, 3))
sns.kdeplot(reference_data, label='reference data', color='#30a2da', ax=axs[0])
sns.kdeplot(test_data, label='test data', color='red', ax=axs[0])
axs[0].set_title('Distribution Comparison')
axs[0].set_ylabel('Density')
axs[0].legend()
sns.ecdfplot(reference_data, label='reference data', color='#30a2da', ax=axs[1])
sns.ecdfplot(test_data, label='test data', color='red', ax=axs[1])
axs[1].set_title('Cumulative Distribution Comparison')
axs[1].set_ylabel('Cumulative Probability')
axs[1].legend()
plt.show();
The statistical tests and visualizations shown above indicate a clear difference between the distributions, even though we know that no drift is actually present. This highlights the importance of using methods specifically designed for time series data, since traditional statistical tests may yield misleading results due to the temporal dependencies and recurring patterns inherent in such data.
Distance-Based framework for temporal drift detection¶
This framework implements a distance-based, data-driven approach to detect temporal drift — changes in the underlying data distribution over time — within time series data. It constructs an empirical baseline of normal behavior from historical (reference) data and uses it to assess whether newly observed data deviates significantly from the established norm.
The approach is both model-agnostic and distance-agnostic: any statistical distance or divergence measure that quantifies dissimilarity between data samples can be employed (e.g., Kolmogorov–Smirnov, Chi-squared, Jensen–Shannon divergence, or other appropriate metrics).
1. Reference Phase — Estimating the Empirical Distribution¶
The first step is to characterize the natural variability of the time series under stable conditions.
Select a reference window
Choose a historical segment of the time series that represents stable and drift-free behavior. This segment serves as the reference dataset.Segment the reference data
Divide the reference time series into non-overlapping chunks of equal length:
Each chunkCompute pairwise distances
For each chunk
This produces a collection of distances:Build the empirical distribution
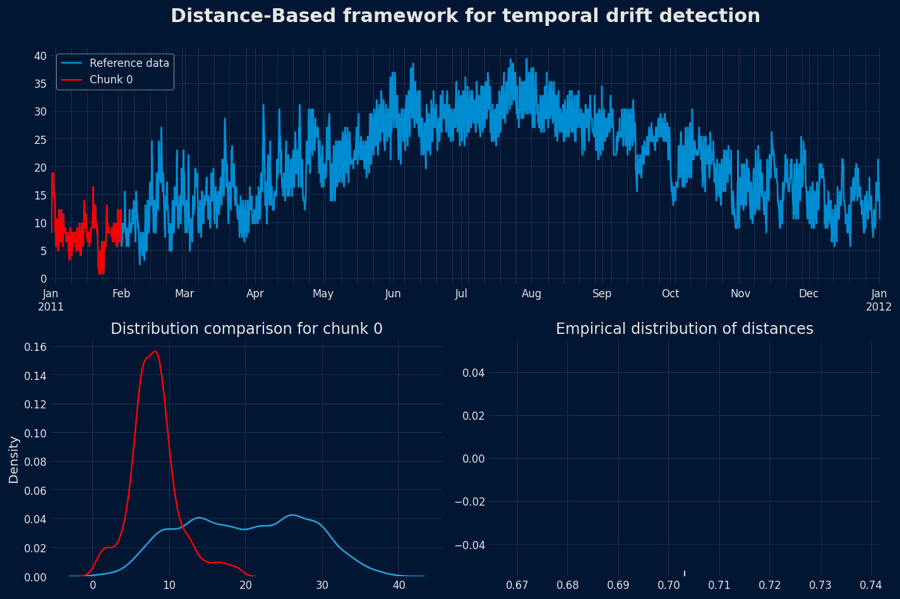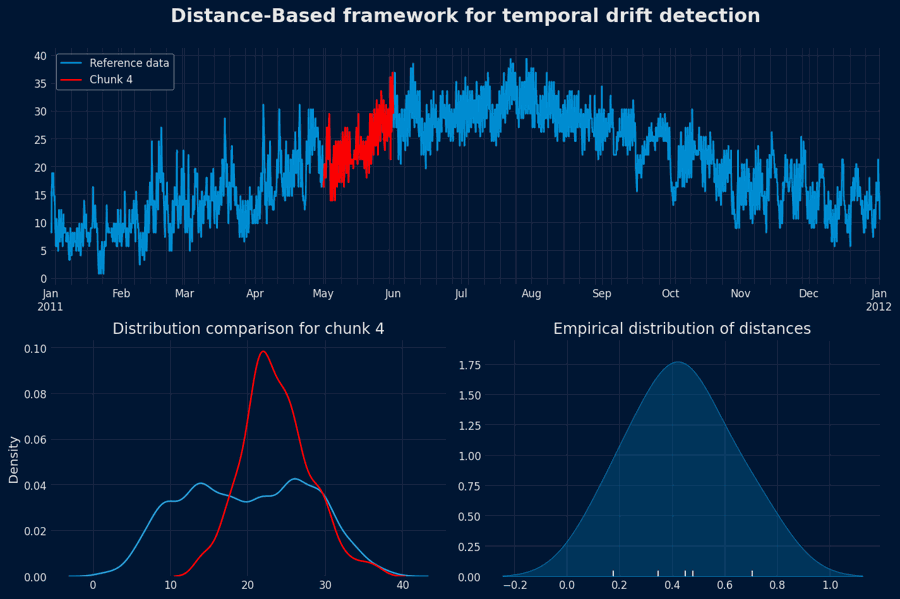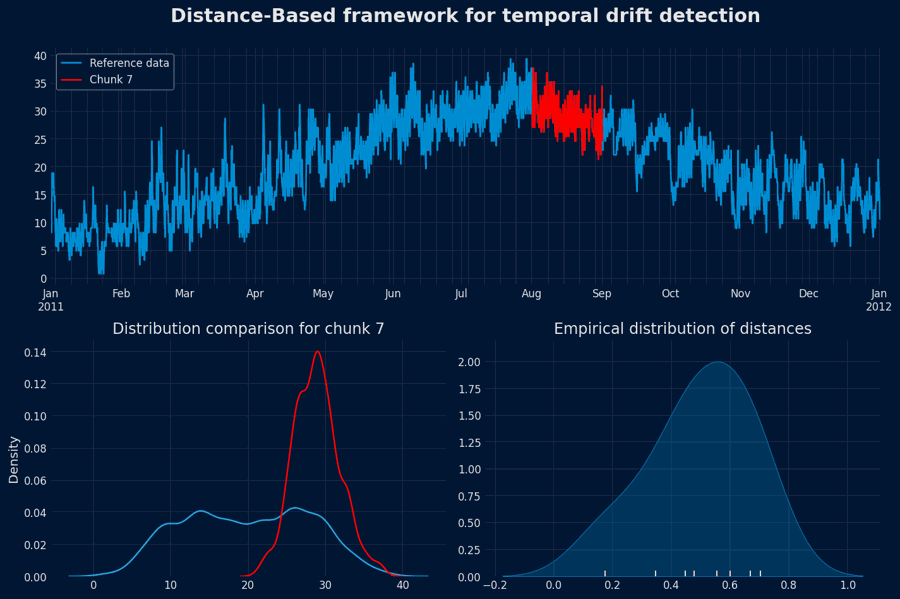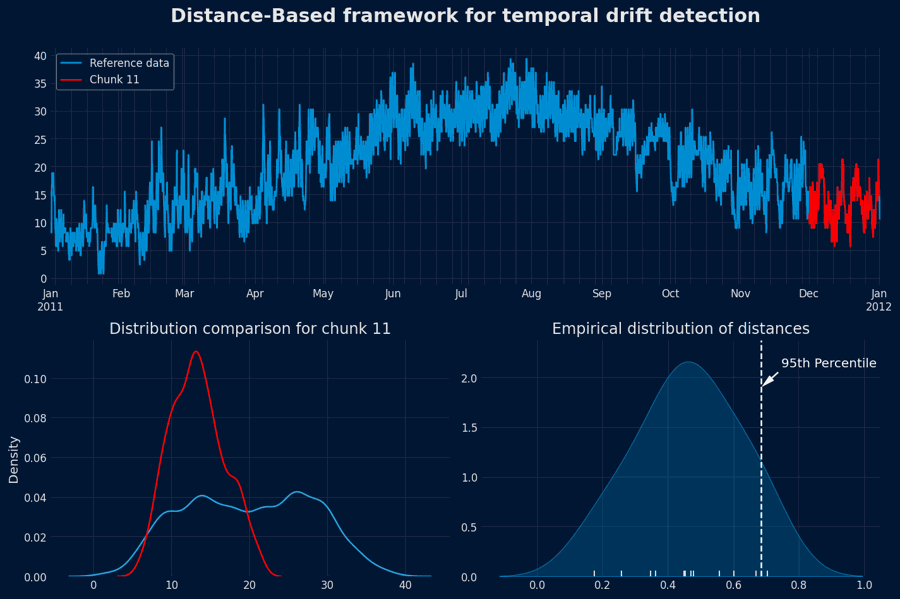
The setDefine a drift threshold
Select a quantile (e.g., the 95th percentile) from the empirical distribution
Any distance greater than
Population Drift Detection - Animation
2. Monitoring Phase — Detecting Drift in New Data¶
Once the baseline distribution is established, new data can be continuously evaluated for drift.
Chunk new data
As new observations become available, segment them into chunks of the same length used in the reference phase:Compute distances to the reference
For each new chunkCompare against the threshold
- If
- If
- If
Interpretation
A flagged chunk suggests that the new data segment differs significantly from historical norms, implying a possible population drift or concept shift. Such cases may warrant further investigation, model retraining, or data pipeline adjustments.