Probabilistic forecasting: prediction intervals and prediction distribution¶
When trying to anticipate future values, most forecasting models focus on predicting the most likely value, which is called point-forecasting. Although knowing the expected value of a time series is useful for most business cases, this type of forecasting does not provide any information about the model's confidence or the prediction's uncertainty.
Probabilistic forecasting, as opposed to point-forecasting, is a family of techniques that enable the prediction of the expected distribution of the outcome, rather than a single future value. This type of forecasting provides much richer information, as it reports the range of probable values into which the true value may fall, allowing the estimation of prediction intervals.
A prediction interval is the interval within which the true value of the response variable is expected to be found with a given probability. There are multiple ways to estimate prediction intervals, most of which require that the residuals (errors) of the model follow a normal distribution. However, when this assumption cannot be made, two commonly used alternatives are bootstrapping and quantile regression.
To illustrate how skforecast enables the estimation of prediction intervals for multi-step forecasting, examples attempting to predict energy demand for a 7-day horizon are provided. Two strategies are showcased:
Prediction intervals based on bootstrapped residuals.
Prediction intervals based on quantile regression.
Warning
As Rob J Hyndman explains in his blog, in real-world problems, almost all prediction intervals are too narrow. For example, nominal 95% intervals may only provide coverage between 71% and 87%. This is a well-known phenomenon and arises because they do not account for all sources of uncertainty. With forecasting models, there are at least four sources of uncertainty:
- The random error term
- The parameter estimates
- The choice of model for the historical data
- The continuation of the historical data generating process into the future
When producing prediction intervals for time series models, generally only the first of these sources is taken into account. Therefore, it is advisable to use test data to validate the empirical coverage of the interval and not solely rely on the expected coverage.
Predicting distribution and intervals using bootstrapped residuals¶
The error of a one-step-ahead forecast is defined as the difference between the actual value and the predicted value ($e_t = y_t - \hat{y}_{t|t-1}$). By assuming that future errors will be similar to past errors, it is possible to simulate different predictions by taking samples from the collection of errors previously seen in the past (i.e., the residuals) and adding them to the predictions.
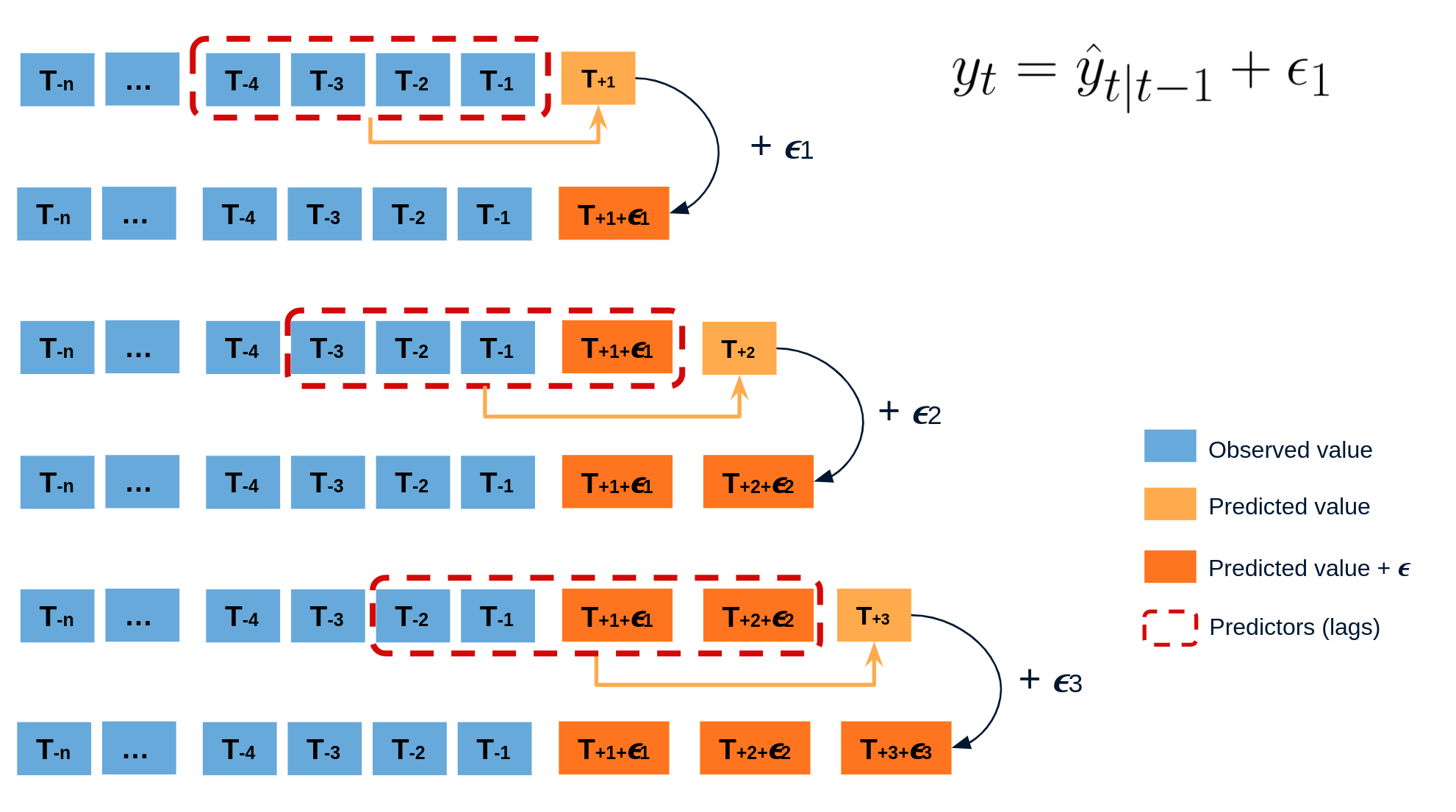
Repeatedly performing this process creates a collection of slightly different predictions, which represent the distribution of possible outcomes due to the expected variance in the forecasting process.
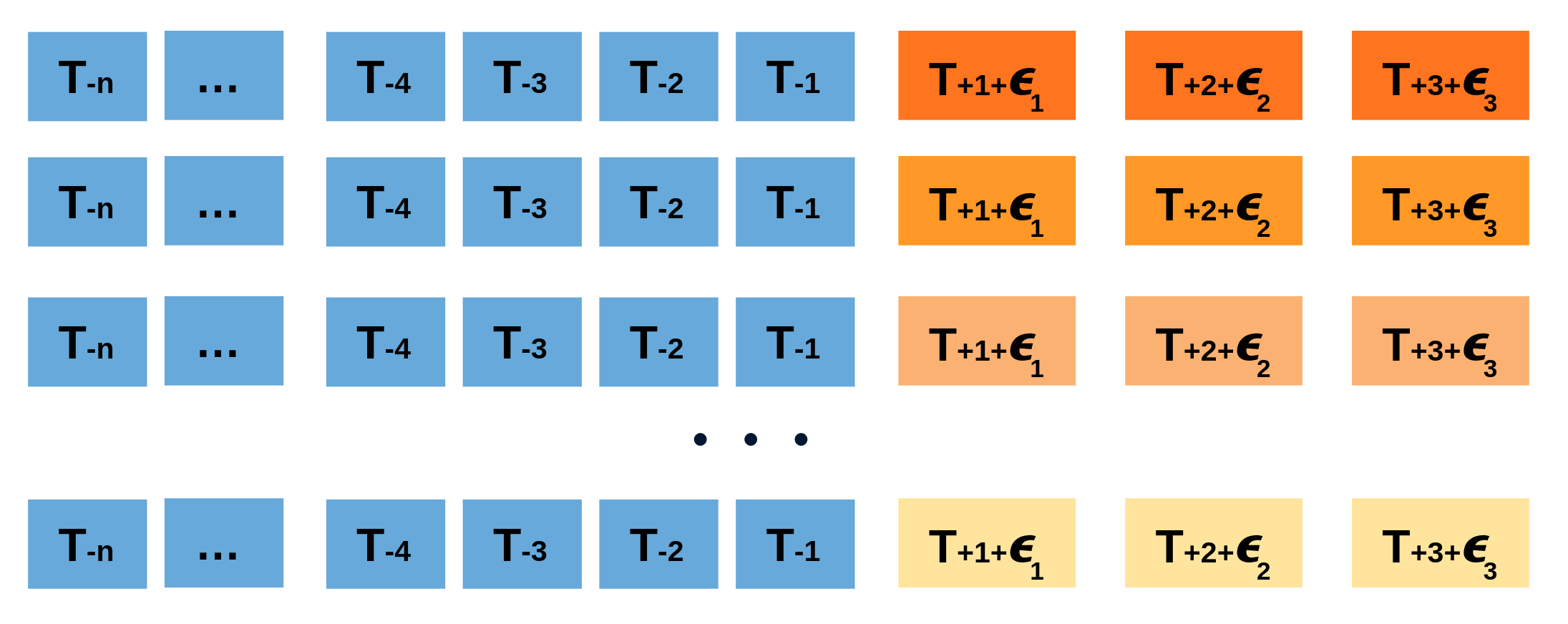
Using the outcome of the bootstrapping process, prediction intervals can be computed by calculating the $α/2$ and $1 − α/2$ percentiles at each forecasting horizon.
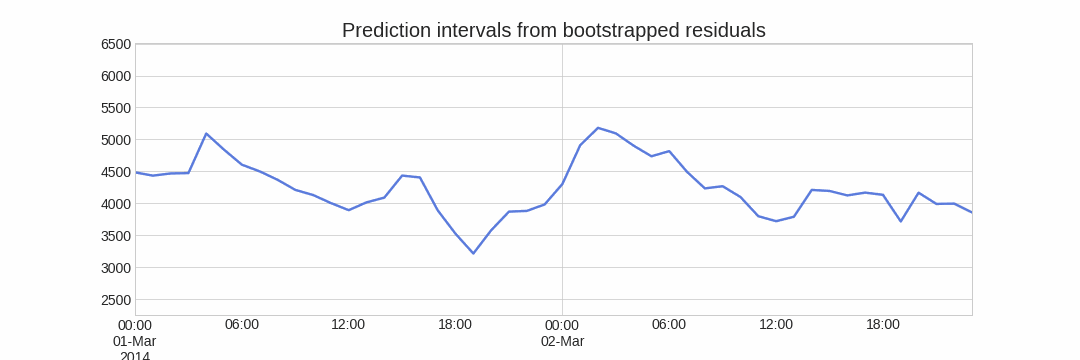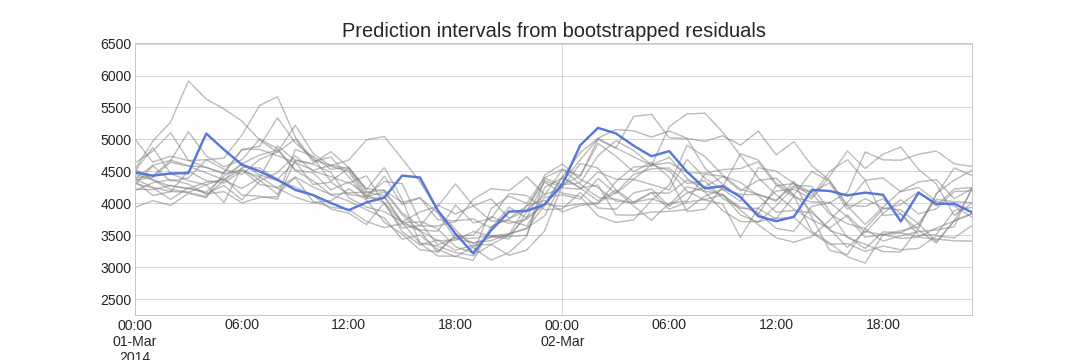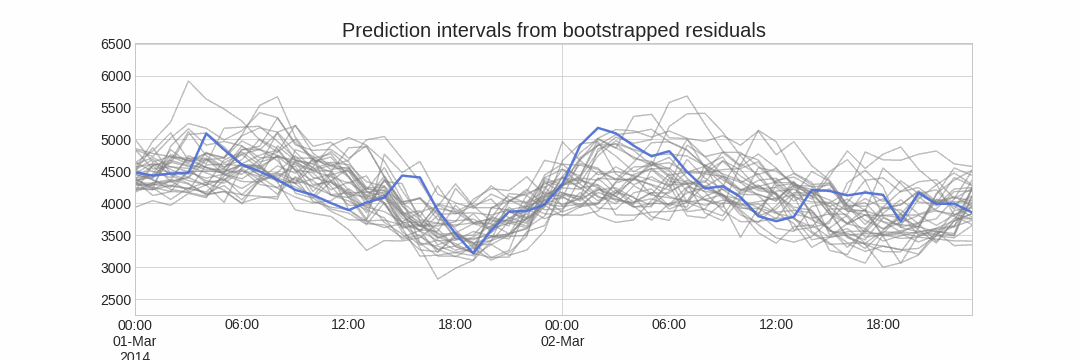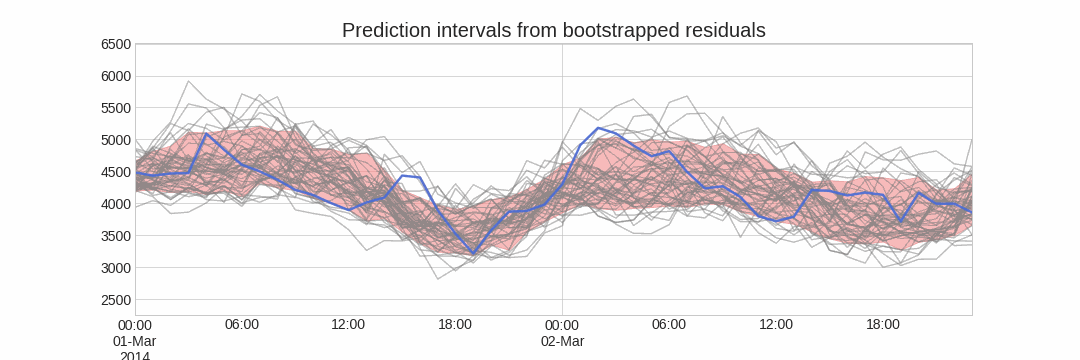
Alternatively, it is also possible to fit a parametric distribution for each forecast horizon.
One of the main advantages of this strategy is that it requires only a single model to estimate any interval. However, performing hundreds or thousands of bootstrapping iterations can be computationally expensive and may not always be feasible.
In skforecast, all forecasters have three different methods that allow for probabilistic forecasting:
predict_bootstrapping: this method generates multiple forecasting predictions through a bootstrapping process. By sampling from a collection of past observed errors (the residuals), each bootstrapping iteration generates a different set of predictions. The output is apandas DataFramewith one row for each predicted step and one column for each bootstrapping iteration.predict_intervals: this method estimates quantile predictions intervals using the values generated withpredict_bootstrapping.predict_dist: this method fits a parametric distribution using the values generated withpredict_bootstrapping. Any of the continuous distributions available in scipy.stats can be used.
The following example demonstrates how to use these methods with a ForecasterAutoreg (note that this also works for all other types of forecasters).
# Data processing
# ==============================================================================
import numpy as np
import pandas as pd
# Plots
# ==============================================================================
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
plt.style.use('fivethirtyeight')
plt.rcParams['lines.linewidth'] = 1.5
dark_style = {
'figure.facecolor' : '#212946',
'axes.facecolor' : '#212946',
'savefig.facecolor' : '#212946',
'axes.grid' : True,
'axes.grid.which' : 'both',
'axes.spines.left' : False,
'axes.spines.right' : False,
'axes.spines.top' : False,
'axes.spines.bottom': False,
'grid.color' : '#2A3459',
'grid.linewidth' : '1',
'text.color' : '0.9',
'axes.labelcolor' : '0.9',
'xtick.color' : '0.9',
'ytick.color' : '0.9',
'font.size' : 12
}
plt.rcParams.update(dark_style)
# Modelling and Forecasting
# ==============================================================================
from skforecast.ForecasterAutoreg import ForecasterAutoreg
from skforecast.ForecasterAutoregDirect import ForecasterAutoregDirect
from skforecast.plot import plot_prediction_distribution
from skforecast.model_selection import backtesting_forecaster
from skforecast.model_selection import grid_search_forecaster
from lightgbm import LGBMRegressor
from sklearn.metrics import mean_pinball_loss
from skforecast.exceptions import LongTrainingWarning
# Configuration
# ==============================================================================
import warnings
warnings.filterwarnings('once')
# Data download
# ==============================================================================
url = (
'https://raw.githubusercontent.com/JoaquinAmatRodrigo/skforecast/master/'
'data/vic_elec.csv'
)
data = pd.read_csv(url, sep=',')
# Data preparation (aggregation at daily level)
# ==============================================================================
data['Time'] = pd.to_datetime(data['Time'], format='%Y-%m-%dT%H:%M:%SZ')
data = data.set_index('Time')
data = data.asfreq('30min')
data = data.sort_index()
data = data.drop(columns='Date')
data = data.resample(rule='D', closed='left', label ='right')\
.agg({'Demand': 'sum', 'Temperature': 'mean', 'Holiday': 'max'})
# Split data into train-validation-test
# ==============================================================================
data = data.loc['2012-01-01 00:00:00': '2014-12-30 23:00:00']
end_train = '2013-12-31 23:59:00'
end_validation = '2014-9-30 23:59:00'
data_train = data.loc[: end_train, :].copy()
data_val = data.loc[end_train:end_validation, :].copy()
data_test = data.loc[end_validation:, :].copy()
print(
f"Train dates : {data_train.index.min()} --- {data_train.index.max()}"
f" (n={len(data_train)})"
)
print(
f"Validation dates : {data_val.index.min()} --- {data_val.index.max()}"
f" (n={len(data_val)})"
)
print(
f"Test dates : {data_test.index.min()} --- {data_test.index.max()}"
f" (n={len(data_test)})"
)
Train dates : 2012-01-01 00:00:00 --- 2013-12-31 00:00:00 (n=731) Validation dates : 2014-01-01 00:00:00 --- 2014-09-30 00:00:00 (n=273) Test dates : 2014-10-01 00:00:00 --- 2014-12-30 00:00:00 (n=91)
# Plot time series partition
# ==============================================================================
fig, ax = plt.subplots(figsize=(9, 3))
data_train['Demand'].plot(label='train', ax=ax)
data_val['Demand'].plot(label='validation', ax=ax)
data_test['Demand'].plot(label='test', ax=ax)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_ylim(bottom=160_000)
ax.set_ylabel('MW')
ax.set_xlabel('')
ax.set_title('Energy demand')
ax.legend();
# Create and train a ForecasterAutoreg
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = LGBMRegressor(
learning_rate = 0.01,
max_depth = 10,
n_estimators = 500,
random_state = 123
),
lags = 7
)
forecaster.fit(y=data.loc[end_train:end_validation, 'Demand'])
forecaster
=================
ForecasterAutoreg
=================
Regressor: LGBMRegressor(learning_rate=0.01, max_depth=10, n_estimators=500,
random_state=123)
Lags: [1 2 3 4 5 6 7]
Transformer for y: None
Transformer for exog: None
Window size: 7
Weight function included: False
Exogenous included: False
Type of exogenous variable: None
Exogenous variables names: None
Training range: [Timestamp('2014-01-01 00:00:00'), Timestamp('2014-09-30 00:00:00')]
Training index type: DatetimeIndex
Training index frequency: D
Regressor parameters: {'boosting_type': 'gbdt', 'class_weight': None, 'colsample_bytree': 1.0, 'importance_type': 'split', 'learning_rate': 0.01, 'max_depth': 10, 'min_child_samples': 20, 'min_child_weight': 0.001, 'min_split_gain': 0.0, 'n_estimators': 500, 'n_jobs': -1, 'num_leaves': 31, 'objective': None, 'random_state': 123, 'reg_alpha': 0.0, 'reg_lambda': 0.0, 'silent': 'warn', 'subsample': 1.0, 'subsample_for_bin': 200000, 'subsample_freq': 0}
fit_kwargs: {}
Creation date: 2023-05-29 13:17:23
Last fit date: 2023-05-29 13:17:23
Skforecast version: 0.8.1
Python version: 3.10.11
Forecaster id: None
Once the Forecaster has been trained, the method predict_bootstraping can be use to simulate n_boot values of the forecasting distribution.
# Predict 10 different forecasting sequences of 7 steps each using bootstrapping
# ==============================================================================
boot_predictions = forecaster.predict_bootstrapping(steps=7, n_boot=10)
boot_predictions
| pred_boot_0 | pred_boot_1 | pred_boot_2 | pred_boot_3 | pred_boot_4 | pred_boot_5 | pred_boot_6 | pred_boot_7 | pred_boot_8 | pred_boot_9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2014-10-01 | 208783.097577 | 204764.999003 | 201367.203420 | 212280.661192 | 204622.100582 | 202889.246579 | 210078.609982 | 210151.742392 | 200990.348257 | 203137.232359 |
| 2014-10-02 | 212340.130913 | 208320.030667 | 217221.147681 | 209996.152477 | 218464.949614 | 212545.697772 | 212061.596039 | 216579.376162 | 226902.326444 | 212847.017644 |
| 2014-10-03 | 221380.131363 | 223890.630246 | 224625.204840 | 207260.018970 | 206099.826214 | 288939.369743 | 220085.831843 | 229514.853352 | 230476.360893 | 224059.729506 |
| 2014-10-04 | 209943.773973 | 212946.528553 | 200027.296792 | 203592.696069 | 194120.730680 | 262225.653280 | 212516.896678 | 222042.271003 | 215236.033624 | 222487.580478 |
| 2014-10-05 | 193372.607408 | 177195.227257 | 194351.934752 | 206606.909536 | 202654.435499 | 297740.735825 | 192454.576530 | 199372.141645 | 208527.690318 | 197830.624380 |
| 2014-10-06 | 199626.367544 | 203338.054671 | 207145.334747 | 208993.695577 | 204766.177714 | 258050.416951 | 184903.916795 | 201473.420885 | 204790.425542 | 183312.907014 |
| 2014-10-07 | 201546.003371 | 212477.910879 | 209639.468951 | 204102.852012 | 225036.945159 | 257847.869040 | 197235.769115 | 196990.134684 | 200007.936217 | 207116.299541 |
Using a ridge plot is a useful way to visualize the uncertainty of a forecasting model. This plot estimates a kernel density for each step by using the bootstrapped predictions.
# Ridge plot of bootstrapping predictions
# ==============================================================================
_ = plot_prediction_distribution(boot_predictions, figsize=(5, 4))
In most cases, the user is interested in a specific interval rather than the entire bootstrapping simulation matrix. To address this need, skforecast provides the predict_interval method. This method internally uses predict_bootstrapping to obtain the bootstrapping matrix and estimates the upper and lower quantiles for each step, thus providing the user with the desired prediction intervals.
# Predict intervals for next 7 steps, quantiles 10th and 90th
# ==============================================================================
predictions = forecaster.predict_interval(steps=7, interval=[10, 90], n_boot=1000)
predictions
| pred | lower_bound | upper_bound | |
|---|---|---|---|
| 2014-10-01 | 205723.923923 | 195483.862851 | 214883.472075 |
| 2014-10-02 | 215167.163121 | 204160.738452 | 225623.750301 |
| 2014-10-03 | 225144.443075 | 212599.136391 | 237675.514362 |
| 2014-10-04 | 211406.440681 | 196863.841123 | 234950.293307 |
| 2014-10-05 | 194848.766987 | 185544.868289 | 225497.131653 |
| 2014-10-06 | 201901.819903 | 188334.486578 | 226720.998742 |
| 2014-10-07 | 208648.526025 | 191797.716429 | 231948.852094 |
The intervals estimated so far are distribution-free, which means that no assumptions are made about a particular distribution. The predict_dist method in skforecast allows fitting a parametric distribution to the bootstrapped prediction samples obtained with predict_bootstrapping. This is useful when there is reason to believe that the forecast errors follow a particular distribution, such as the normal distribution or the student's t-distribution. The predict_dist method allows the user to specify any continuous distribution from the scipy.stats module.
# Predict the parameters of a normal distribution for the next 7 steps
# ==============================================================================
from scipy.stats import norm
predictions = forecaster.predict_dist(steps=7, distribution=norm, n_boot=1000)
predictions
| loc | scale | |
|---|---|---|
| 2014-10-01 | 205374.632063 | 12290.061732 |
| 2014-10-02 | 215791.488070 | 13607.935838 |
| 2014-10-03 | 225631.039103 | 14206.970100 |
| 2014-10-04 | 215210.987777 | 18980.776421 |
| 2014-10-05 | 202613.715687 | 19980.302998 |
| 2014-10-06 | 205391.493409 | 19779.732794 |
| 2014-10-07 | 208579.269999 | 18950.289467 |
Backtesting with prediction intervals¶
A backtesting process can be applied to evaluate the performance of the forecaster over a period of time, for example on test data, and calculate the actual coverage of the estimated range.
# Backtesting on test data
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
steps = 7,
metric = 'mean_squared_error',
initial_train_size = len(data_train) + len(data_val),
fixed_train_size = True,
gap = 0,
allow_incomplete_fold = True,
refit = True,
interval = [10, 90],
n_boot = 1000,
random_state = 123,
verbose = False
)
predictions.head(4)
0%| | 0/13 [00:00<?, ?it/s]
| pred | lower_bound | upper_bound | |
|---|---|---|---|
| 2014-10-01 | 223264.432587 | 214633.692784 | 231376.785240 |
| 2014-10-02 | 233596.210854 | 223051.862727 | 244752.538248 |
| 2014-10-03 | 242653.671597 | 226947.654906 | 258361.695192 |
| 2014-10-04 | 220842.603128 | 209967.438912 | 236404.408845 |
# Interval coverage on test data
# ==============================================================================
inside_interval = np.where(
(data.loc[predictions.index, 'Demand'] >= predictions['lower_bound']) & \
(data.loc[predictions.index, 'Demand'] <= predictions['upper_bound']),
True,
False
)
coverage = inside_interval.mean()
print(f"Coverage of the predicted interval on test data: {100 * coverage}")
Coverage of the predicted interval on test data: 65.93406593406593
# Plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3))
data.loc[end_validation:, 'Demand'].plot(ax=ax, label='Demand')
ax.fill_between(
predictions.index,
predictions['lower_bound'],
predictions['upper_bound'],
color = 'deepskyblue',
alpha = 0.3,
label = '80% interval'
)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_ylabel('MW')
ax.set_xlabel('')
ax.set_title('Energy demand forecast')
ax.legend();
The coverage of the predicted interval is much lower than expected (80%).
Using out-sample-residuals¶
By default, the training residuals are used to create the prediction intervals. However, this is not the most recommended option as the estimated interval tends to be too narrow. This is because the model's performance on training data is usually better than on new observations, leading to smaller residuals and, in turn, narrower prediction intervals.
To overcome this issue, it is advisable to use other residuals, such as those obtained from a validation set. This can be achieved by storing the new residuals inside the forecaster using the set_out_sample_residuals method. Once the new residuals have been added to the forecaster, use in_sample_residuals = False when calling the predict_interval method.
# Backtesting using validation data
# ==============================================================================
metric, backtest_predictions = backtesting_forecaster(
forecaster = forecaster,
y = data.loc[:end_validation, 'Demand'],
initial_train_size = len(data_train),
steps = 7,
refit = True,
metric = 'mean_squared_error',
verbose = False
)
# Calculate residuals in validation data
# ==============================================================================
residuals = (data_val['Demand'] - backtest_predictions['pred']).to_numpy()
residuals[:5]
0%| | 0/39 [00:00<?, ?it/s]
array([-16084.02669559, -14168.47600418, -4416.31618072, -15101.78356121,
-31133.70782794])
Once the residuals of the validation set are calculated, they can be stored inside the forecaster. This allows the forecaster to use the out-of-sample residuals for prediction interval calculation instead of the default in-sample residuals. By doing so, the estimated prediction intervals will be less optimistic and more representative of the performance of the model on new observations.
# Set out-sample residuals
# ==============================================================================
forecaster.set_out_sample_residuals(residuals=residuals)
Finally, a backtesting process is applied to the test data, this time indicating in_sample_residuals = False to use the out-of-sample residuals in the interval estimation.
# Backtesting using test data
# ==============================================================================
metric, predictions_2 = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
steps = 7,
refit = True,
interval = [10, 90],
n_boot = 1000,
in_sample_residuals = False,
random_state = 123,
metric = 'mean_squared_error',
verbose = False
)
predictions_2.head(4)
0%| | 0/13 [00:00<?, ?it/s]
| pred | lower_bound | upper_bound | |
|---|---|---|---|
| 2014-10-01 | 223264.432587 | 203983.457029 | 236841.748720 |
| 2014-10-02 | 233596.210854 | 207273.919217 | 255429.172682 |
| 2014-10-03 | 242653.671597 | 211668.258043 | 265757.229322 |
| 2014-10-04 | 220842.603128 | 195869.206779 | 245921.530106 |
# Interval coverage on test data
# ==============================================================================
inside_interval = np.where(
(data.loc[predictions_2.index, 'Demand'] >= predictions_2['lower_bound']) & \
(data.loc[predictions_2.index, 'Demand'] <= predictions_2['upper_bound']),
True,
False
)
coverage = inside_interval.mean()
print(f"Coverage of the predicted interval on test data: {100 * coverage}")
# Plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3))
data.loc[end_validation:, 'Demand'].plot(ax=ax, label='Demand')
ax.fill_between(
predictions.index,
predictions['lower_bound'],
predictions['upper_bound'],
color = 'orange',
alpha = 0.3,
label = '80% interval in-sample residuals'
)
ax.fill_between(
predictions_2.index,
predictions_2['lower_bound'],
predictions_2['upper_bound'],
color = 'deepskyblue',
alpha = 0.3,
label = '80% interval out-sample residuals'
)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_ylabel('MW')
ax.set_xlabel('')
ax.set_title('Energy demand forecast')
ax.legend(fontsize=10);
Coverage of the predicted interval on test data: 92.3076923076923
Using out-of-sample residuals, the interval coverage is much closer to that expected than when using in-sample residuals.
Note
In the case of ForecasterAutoregDirect, ForecasterAutoregMultiSeries, ForecasterAutoregMultiSeriesCustom and ForecasterAutoregMultiVariate, the residuals must be provided using a dictionary to indicate to which step or level (series) they belong to.
Prediction intervals using quantile regression models¶
As opposed to linear regression, which is intended to estimate the conditional mean of the response variable given certain values of the predictor variables, quantile regression aims at estimating the conditional quantiles of the response variable. For a continuous distribution function, the $\alpha$-quantile $Q_{\alpha}(x)$ is defined such that the probability of $Y$ being smaller than $Q_{\alpha}(x)$ is, for a given $X=x$, equal to $\alpha$. For example, 36% of the population values are lower than the quantile $Q=0.36$. The most known quantile is the 50%-quantile, more commonly called the median.
By combining the predictions of two quantile regressors, it is possible to build an interval. Each model estimates one of the limits of the interval. For example, the models obtained for $Q = 0.1$ and $Q = 0.9$ produce an 80% prediction interval (90% - 10% = 80%).
Several machine learning algorithms are capable of modeling quantiles. Some of them are:
Just as the squared-error loss function is used to train models that predict the mean value, a specific loss function is needed in order to train models that predict quantiles. The most common metric used for quantile regression is calles quantile loss or pinball loss:
$$\text{pinball}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \alpha \max(y_i - \hat{y}_i, 0) + (1 - \alpha) \max(\hat{y}_i - y_i, 0)$$where $\alpha$ is the target quantile, $y$ the real value and $\hat{y}$ the quantile prediction.
It can be seen that loss differs depending on the evaluated quantile. The higher the quantile, the more the loss function penalizes underestimates, and the less it penalizes overestimates. As with MSE and MAE, the goal is to minimize its values (the lower loss, the better).
Two disadvantages of quantile regression, compared to the bootstrap approach to prediction intervals, are that each quantile needs its regressor and quantile regression is not available for all types of regression models. However, once the models are trained, the inference is much faster since no iterative process is needed.
This type of prediction intervals can be easily estimated using ForecasterAutoregDirect and ForecasterAutoregMultiVariate models.
As in the previous example, an 80% prediction interval is estimated for 7 steps-ahead predictions but, this time, using quantile regression. In this example a LightGBM gradient boosting model is trained, however, the reader can use any other model by simply substituting the regressor definition.
# Create forecasters: one for each bound of the interval
# ==============================================================================
# The forecasters obtained for alpha=0.1 and alpha=0.9 produce a 80% confidence
# interval (90% - 10% = 80%).
# Forecaster for quantile 10%
forecaster_q10 = ForecasterAutoregDirect(
regressor = LGBMRegressor(
objective = 'quantile',
metric = 'quantile',
alpha = 0.1,
learning_rate = 0.1,
max_depth = 10,
n_estimators = 100
),
lags = 7,
steps = 7
)
# Forecaster for quantile 90%
forecaster_q90 = ForecasterAutoregDirect(
regressor = LGBMRegressor(
objective = 'quantile',
metric = 'quantile',
alpha = 0.9,
learning_rate = 0.1,
max_depth = 10,
n_estimators = 100
),
lags = 7,
steps = 7
)
forecaster_q10.fit(y=data['Demand'])
forecaster_q90.fit(y=data['Demand'])
Once the quantile forecasters are trained, they can be used to predict each of the bounds of the forecasting interval.
# Predict intervals for next 7 steps
# ==============================================================================
predictions_q10 = forecaster_q10.predict(steps=7)
predictions_q90 = forecaster_q90.predict(steps=7)
predictions = pd.DataFrame({
'lower_bound': predictions_q10,
'upper_bound': predictions_q90,
})
predictions
| lower_bound | upper_bound | |
|---|---|---|
| 2014-12-31 | 177607.329878 | 218885.714906 |
| 2015-01-01 | 178062.602517 | 242582.788349 |
| 2015-01-02 | 186213.019530 | 220677.491829 |
| 2015-01-03 | 184901.085939 | 204261.638256 |
| 2015-01-04 | 193237.899189 | 235310.200573 |
| 2015-01-05 | 196673.050873 | 284881.068713 |
| 2015-01-06 | 184148.733152 | 293018.478848 |
When validating a quantile regression model, a custom metric must be provided depending on the quantile being estimated. These metrics will be used again when tuning the hyper-parameters of each model.
# Loss function for each quantile (pinball_loss)
# ==============================================================================
def mean_pinball_loss_q10(y_true, y_pred):
"""
Pinball loss for quantile 10.
"""
return mean_pinball_loss(y_true, y_pred, alpha=0.1)
def mean_pinball_loss_q90(y_true, y_pred):
"""
Pinball loss for quantile 90.
"""
return mean_pinball_loss(y_true, y_pred, alpha=0.9)
# Backtesting on test data
# ==============================================================================
warnings.simplefilter('ignore', category=LongTrainingWarning)
metric_q10, predictions_q10 = backtesting_forecaster(
forecaster = forecaster_q10,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
steps = 7,
refit = True,
metric = mean_pinball_loss_q10,
verbose = False
)
metric_q90, predictions_q90 = backtesting_forecaster(
forecaster = forecaster_q90,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
steps = 7,
refit = True,
metric = mean_pinball_loss_q90,
verbose = False
)
0%| | 0/13 [00:00<?, ?it/s]
0%| | 0/13 [00:00<?, ?it/s]
Predictions generated for each model are used to define the upper and lower limits of the interval.
# Interval coverage on test data
# ==============================================================================
inside_interval = np.where(
(data.loc[end_validation:, 'Demand'] >= predictions_q10['pred']) & \
(data.loc[end_validation:, 'Demand'] <= predictions_q90['pred']),
True,
False
)
coverage = inside_interval.mean()
print(f"Coverage of the predicted interval: {100 * coverage}")
Coverage of the predicted interval: 61.53846153846154
The coverage of the predicted interval is much lower than expected (80%).
The hyperparameters of the model were hand-tuned and there is no reason that the same hyperparameters are suitable for the 10th and 90th percentiles regressors. Therefore, a grid search is carried out for each forecaster.
# Grid search of hyper-parameters and lags for each quantile forecaster
# ==============================================================================
# Regressor hyper-parameters
param_grid = {
'n_estimators': [100, 500],
'max_depth': [3, 5, 10],
'learning_rate': [0.01, 0.1]
}
# Lags used as predictors
lags_grid = [7]
results_grid_q10 = grid_search_forecaster(
forecaster = forecaster_q10,
y = data.loc[:end_validation, 'Demand'],
param_grid = param_grid,
lags_grid = lags_grid,
steps = 7,
refit = False,
metric = mean_pinball_loss_q10,
initial_train_size = int(len(data_train)),
return_best = True,
verbose = False
)
results_grid_q90 = grid_search_forecaster(
forecaster = forecaster_q90,
y = data.loc[:end_validation, 'Demand'],
param_grid = param_grid,
lags_grid = lags_grid,
steps = 7,
refit = False,
metric = mean_pinball_loss_q90,
initial_train_size = int(len(data_train)),
return_best = True,
verbose = False
)
Number of models compared: 12.
lags grid: 0%| | 0/1 [00:00<?, ?it/s]
params grid: 0%| | 0/12 [00:00<?, ?it/s]
`Forecaster` refitted using the best-found lags and parameters, and the whole data set:
Lags: [1 2 3 4 5 6 7]
Parameters: {'learning_rate': 0.01, 'max_depth': 3, 'n_estimators': 500}
Backtesting metric: 2713.0192469016706
Number of models compared: 12.
lags grid: 0%| | 0/1 [00:00<?, ?it/s]
params grid: 0%| | 0/12 [00:00<?, ?it/s]
`Forecaster` refitted using the best-found lags and parameters, and the whole data set:
Lags: [1 2 3 4 5 6 7]
Parameters: {'learning_rate': 0.01, 'max_depth': 10, 'n_estimators': 500}
Backtesting metric: 4094.3047516967745
Once the best hyperparameters have been found for each forecaster, a backtesting process is applied again using the test data.
# Backtesting on test data
# ==============================================================================
metric_q10, predictions_q10 = backtesting_forecaster(
forecaster = forecaster_q10,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
steps = 7,
refit = False,
metric = mean_pinball_loss_q10,
verbose = False
)
metric_q90, predictions_q90 = backtesting_forecaster(
forecaster = forecaster_q90,
y = data['Demand'],
initial_train_size = len(data_train) + len(data_val),
steps = 7,
refit = False,
metric = mean_pinball_loss_q90,
verbose = False
)
0%| | 0/13 [00:00<?, ?it/s]
0%| | 0/13 [00:00<?, ?it/s]
# Plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 3))
data.loc[end_validation:, 'Demand'].plot(ax=ax, label='Demand')
ax.fill_between(
data.loc[end_validation:].index,
predictions_q10['pred'],
predictions_q90['pred'],
color = 'deepskyblue',
alpha = 0.3,
label = '80% interval'
)
ax.yaxis.set_major_formatter(ticker.EngFormatter())
ax.set_ylabel('MW')
ax.set_xlabel('')
ax.set_title('Energy demand forecast')
ax.legend();
# Interval coverage
# ==============================================================================
inside_interval = np.where(
(data.loc[end_validation:, 'Demand'] >= predictions_q10['pred']) & \
(data.loc[end_validation:, 'Demand'] <= predictions_q90['pred']),
True,
False
)
coverage = inside_interval.mean()
print(f"Coverage of the predicted interval: {100 * coverage}")
Coverage of the predicted interval: 75.82417582417582
After optimizing the hyper-parameters of each quantile forecaster, the coverage is closer to the expected one (80%).
%%html
<style>
.jupyter-wrapper .jp-CodeCell .jp-Cell-inputWrapper .jp-InputPrompt {display: none;}
</style>